Ce programme est conçu pour résoudre les problèmes courants de thermomécanique et de transfert de chaleur que les ingénieurs rencontrent fréquemment.
Le programme aborde les domaines suivants :
1. Énergie : Chauffage et refroidissement, changement de phase, pouvoir calorifique des combustibles
2. Gaz parfait : État et changement d'état, système thermodynamique
3. Transfert de chaleur à travers des parois composites : Conduction, rayonnement, convection
4. Solutions pour les parois à ailettes et les faisceaux de tubes
5. Changement de température longitudinal dans les tuyauteries : Changement de température et temps de refroidissement dans les réservoirs
6. Échangeurs de chaleur
7. Transfert de chaleur par rayonnement
8. Puissance du rayonnement solaire : Durée, temps, position, environnement, orientation de la surface, etc.
9. Préparation des données pour l'utilisation du complément "Solveur"
Les calculs incluent des centaines de matériaux, liquides et gaz prédéfinis, un tableau périodique des éléments, des conversions d'unités, et bien plus encore. Un grand nombre d'exemples résolus sont également disponibles.
Les calculs utilisent des données, des procédures, des algorithmes et des informations issus de la littérature spécialisée, des normes et des catalogues d'entreprise.
[01] YUNUS A. ÇENGEL, AFSHIN J. GHAJAR: Heat and Mass Transfer: Fundamentals
& Applications, 5th Edition, McGraw-Hill Education.
[02] YUNUS A. ÇENGEL: Heat Transfer a Practical Approach, Second Edition.
[03] MORAN, M.J., SHAPIO, H.N.: Fundamentals of engineering thermodynamics. 8th
Edition New York: John Wiley a sons, 1990.
[04] DEWITT, BERGMAN, LAVINE: Fundamentals of Heat and Mass Transfer 6th Edition
[05] WARREN M.ROHSENOW, JAMES R.HARTNETT, YOUNG I.CHO: Handbook of Heat
Transfer, 3th Edition, McGraw-Hill
[06] SCHLUNDER, BELL, HEWITT, SPALDING: Heat Exchanger
Design Handbook, VDI-Verlag GmbH, 1983.
[07] LOIS THEODORE: Heat Transfer Applications for the
Practicing Engineer, John Wiley & Sons, Inc., 2011.
[08] MYER KUTZ: Heat-Transfer Calculations,
McGraw-Hill
[09] HOLMAN, J.P.: Heat Transfer, 10th. Edition, New
York: McGraw-Hill
[10] HOLMAN, J.P. Thermodynamics. 4th. New York:
McGraw-Hill Book Company, 1988. 780 s. ISBN 0-07-029633-2.
[11] MOHAMED M. EL-AWAD: Optimisation Analyses of
Fluid- Thermal Systems Using Excel,
[12] FRANK KREITH, RAJ MANGLIK, MARK BOHN: Principles
of Heat Transfer, Cengage Learning, Inc., 2011
[13] HORÁK VLADIMÍR, STŘEDA IVO: Mechanika tekutin
- Termomechanika, Strojírenská příručka, Scientia sro.
[14] RANEVI,K. Termodynamické tabulky. 1.vyd.
Bratislava: ALFA 1984. 313s. [L5] HAEK, P. Tabulky pro tepelnou techniku. 1
.vyd. VB Ostrava, 1980, 247 s.
[15] SAZIMA,M., KMON1OEK,V., SCHNELER,J. Teplo. 1.vyd.
Praha: SNTL, 1989. 588 s. Technický průvodce. ISBN 80-03-00043-2.
[16] M.A.MICHEJEV: Základy sdílení tepla, Průmyslové
vydavatelství, 1952
[17] PETRAK,J., DVOAK, Z., KLAZAR, L., SYNEK, V.
Chiadivo R134a, (1.vyd.) VUT, 1993. 72s.
[18] MIROSLAV JÍLEK, ZDENĚK RANDA: Termomechanika -
sbírka příkladů, ČVUT, 2004
L'information sur la syntaxe et la commande du calcul peut être trouvée dans le document "commande, structure et syntaxe des calculs".
L'information sur le but, l'utilisation et la commande du paragraphe "information sur le projet" peut être trouvée dans le document "information sur le projet".
E = m * ΔT
* Cp
E ... Énergie [J]
m ... Masse [kg]
ΔT
... Changement de température [K]
Cp ... Capacité thermique spécifique [J/kg/K]
EM
= m * CpM
* 1000
EB
= m * CpB
* 1000
EM, EB
... Énergie [J]
CpM
... Capacité thermique spécifique de fusion [kJ/kg]
CpB
... Capacité thermique spécifique d'ébullition [kJ/kg]
E = m * HHV
* (η / 100) * 1000000
E ... Énergie [J]
m ... Masse du combustible brûlé [kg]
HHV
... Chaleur de combustion [MJ/kg]
η ... Efficacité de combustion [%]
L'état d'un système thermodynamique est caractérisé par des variables d'état. La relation entre ces variables d'état est définie par des équations d'état.
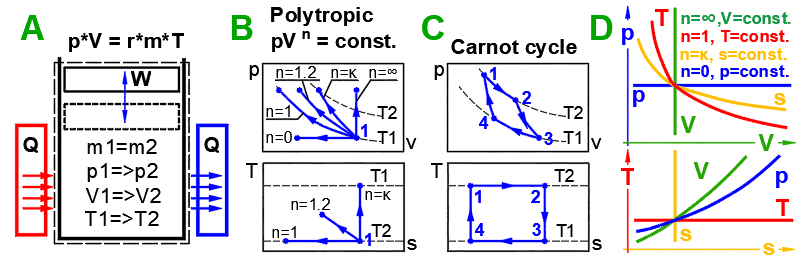
A ... Un exemple de système thermodynamique simple, le gaz parfait, suit l'équation : p*V=m*r*T.
B ... Les processus réversibles peuvent être décrits plus généralement comme des
processus polytropiques,
où la capacité thermique d'un système fermé reste constante. Dans un processus polytropique,
toutes les variables d'état (p,V,T)
changent généralement. Pour un processus polytropique
dans un gaz parfait, l'équation p*V^n = const.
s'applique. Les diagrammes p-V et T-s montrent les courbes de changement pour
différentes valeurs de n.
C ... Cycle de Carnot. Un exemple de machine thermique idéale composée de deux
processus isothermes et de deux processus adiabatiques.
D ... Courbes des changements d'état réversibles fondamentaux.
p * V = m * r * T
r = R / M
M = m / N
p ... Pression absolue [Pa]
V ... Volume [m^3]
m ... Masse [kg]
T ... Température [°K]
R ... Constante universelle des gaz R=8314.46261815324 [J/kmol/K]
M ... Masse molaire du gaz [kg/kmol]
(air 28.966 kg/kmol)
N ... Quantité de substance [kmol]
r ... Constante spécifique du gaz [J/kg/K] (air 287.0427 J/kg/K)
u = u0 + cv * (T - T0) [J/kg]
Δu = cv * (T2 - T1) [J/kg]
h = h0 + cp * (T - T0) [J/kg]
Δh = cp * (T2 - T1) [J/kg]
ds = s2 - s1 = cp * Ln(T2/T1) - r * Ln(p2 / p1)
ds = s2 - s1 = cv * Ln(T2/T1) + r * Ln(v2 / v1)
cp
- cv = r
cp ... Capacité thermique spécifique - pression constante [J/kg/K]
cv ... Capacité thermique spécifique - volume constant [J/kg/K]
κ = cp
/ cv
cv = r / (κ - 1)
cp
= κ * cv
p1 * V1 = p2 * V2
V1 / V2 = T1 / T2
Les processus réversibles peuvent être considérés comme des processus polytropiques plus généraux pour lesquels :
p * V^n = constante
T2 / T1 = (V1 / V2)^(n-1) = (p2 / p1)^((n-1)/n)
n ... Exposant polytropique
[~]
Pour des valeurs choisies de n alors :
n=0 , p=const,
Isobarique, (dp=0, wt=0,
q=Δh,
w=Δh-Δu)
n=1 , T=const, Isothermique,
(dT=0, Δu=Δh=0,
q=w=wt)
n=κ , s=const, Isoentropic,
(ds=0,
q=0, w=-Δu, wt=-Δh)
n=∞ , v=const, Isochoric,
(dv=0,
w=0, q=Δu, wt=Δu-Δh)
n = ln(p2 / p1) / (ln(p2 / p1) - ln(T2 / T1))
n = (ln(V2 / V1) - ln(T2 / T1)) / ln(V2 / V1)
q = cn
* (T2 - T1) [J/kg]
cn
= cv * (n - κ) / (n - 1)
cn
... Capacité thermique spécifique polytropique
[J/kg/K]
w = q - Δu [J/kg]
wt = q - Δh = n * w [J/kg]
Calcul des paramètres d'un gaz qui
est introduit par le mélange de deux parties avec des paramètres différents p,V,T.
m = m1 + m2
p = m / M * R * T / V
V = V1 + V2
T = (m1 * T1 + m2 * T2) / (m1 + m2)
C'est un problème fréquemment rencontré, tant en ingénierie mécanique que dans d'autres domaines connexes. Bien entendu, cette problématique peut être résolue à l'aide de logiciels de simulation appropriés. Néanmoins, pour une estimation de base et une grande partie de ces tâches, un simple calcul basé sur des relations physiques fondamentales est généralement suffisant.
Le transfert de chaleur est classé en conduction, convection et rayonnement. Les relations pertinentes sont présentées ci-dessous.
Dans les calculs, les relations suivantes sont utilisées pour les parois planes, cylindriques et sphériques composées (max. 10 couches).
r(i) = D(i) / 2
q' = -λ * ΔT [W/m²]
qp'
= (t(1) - t(n+1)) / Rp
qp'
= (t(1) - t(n+1)) / Σ (b(i) / λ(i)) ..... [i=1...n]
R = Rp = Σ (b(i) / λ(i)) ..... [i=1...n]
qc'
= (t(1) - t(n+1)) / Rc
qc'
= (t(1) - t(n+1)) / (1/(2 * 3,14) * Σ ((1/λ(i)) * ln(r(i+1)/r(i)))) .....
[i=1...n]
Rc = (1 / (2 * 3.14159) * Σ ((1/λ(i)) * ln(r(i+1)/r(i)))) ..... [i=1...n]
R = Rc * (2 * 3.14159 * r(1))
qs'
= (t(1) - t(n+1)) / Rs
qs'
= (t(1) - t(n+1)) / (1/(4 * 3,14) * Σ ((1/λ(i)) * (1/r(i) - 1/r(i+1))) .....
[i=1...n]
Rs = (1 / (4 * 3.14159) * Σ ((1/λ(i)) * (1/r(i) - 1/r(i+1))) ..... [i=1...n]
R = Rs * (4 * 3.14159 * r(1)²)
Le transfert de chaleur se produit dans la couche limite près d'une paroi, qui se forme en raison des différences de température. Le transfert de chaleur lui-même dépend alors d'une variété de paramètres (propriétés du fluide, type d'écoulement, géométrie de la surface, etc.).
Pour la convection forcée (où le milieu est entraîné) et la convection naturelle, de nombreuses équations basées sur des mesures et des approximations sont disponibles (voir littérature). Les plus importantes et fréquemment utilisées sont employées dans ce calcul. Ces équations, leurs plages de validité et les graphiques correspondants sont fournis ci-dessous. Pour les graphiques, des valeurs dimensionnelles qui peuvent correspondre à une utilisation courante ont été choisies. Dans les graphiques, l'air et l'eau, en tant que milieux de travail les plus courants, sont choisis pour comparaison.
Pour les graphiques, les unités suivantes ont été choisies : Température [°C], Dimensions [mm].
Nombres Adimensionnels La plupart des relations utilisées sont des équations empiriques, les résultats étant exprimés par des dépendances de critères de similarité adimensionnels.
Nombre de Grashofer Gr = 9.81 * L * β
* abs(T - Ts) / ν
Nombre de Nusselt Nu = hc * L / λ
Nombre de Prandtl Pr = (µ / Rho) / (λ / (Cp * Rho))
Nombre de Rayleigh Ra = Gr * Pr
Nombre de Reynolds Re = (L * V) / ν
Coefficient de transfert thermique par convection
En général, la formule suivante est utilisée :
hc = (Nu * λ) / L
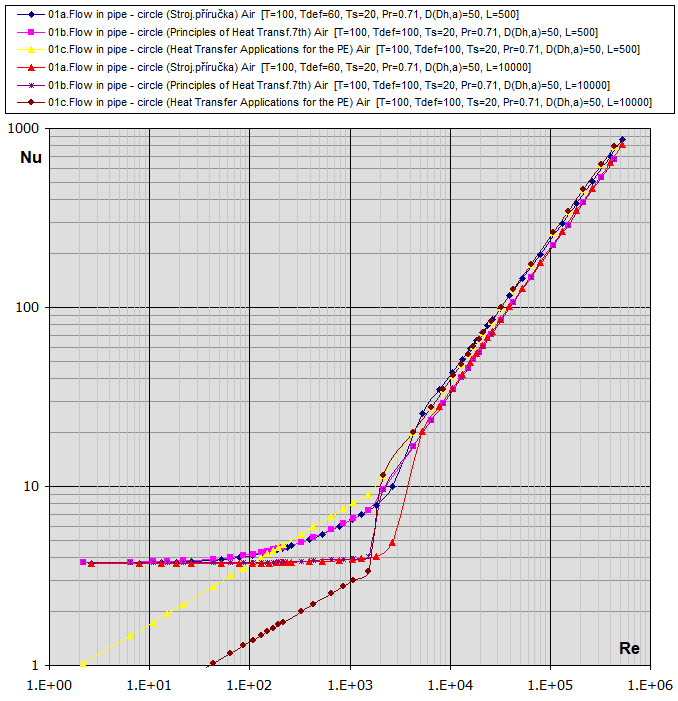
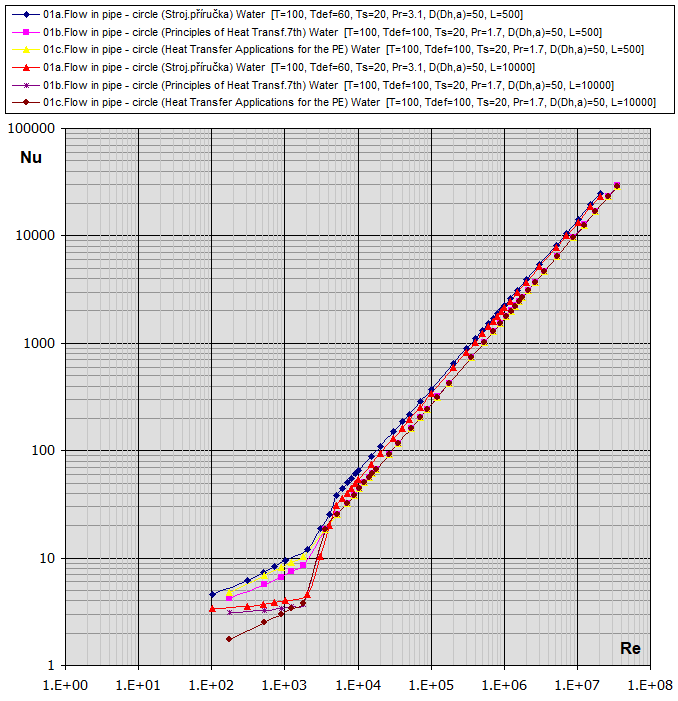
01a. Écoulement en conduite
- Section circulaire
(D,L) : [Tdef = (T+Ts)/2, 0.1<Re<1e7] ...
(Strojírenská příručka, Graetz)
hc = (Nu *
λ) / D
Nu = (3.65 + (0.0668 * Re * Pr * (D/L)) / (1 + 0.045 * (Re * Pr *
(D/L))^(2/3))) * (μ / μs)^0.14 ..... [Re<2300]
Nu = 21 * (Pr * (D/L))^0.33 * (Re/2300)^(LOG(L/D)) ..... [Re*Pr*(D/L)>12, Pr>0.5,
L/D>30, 2300<Re<5000]
Nu = 3.66 * (Re/2300)^(2.3 + LOG(Pr) ..... [Re*Pr*(D/L)<12, Pr>0.5, L/D>30,
2300<Re<5000]
Nu = E * (0.023 * Pr^H * Re^0.8) * K ..... [0.5<Ts/Tdef<1 (°K),
1e4<Re<2e6]
Nu = E * (0.023 * Pr^H * Re^0.8) * K ..... [1<Ts/Tdef<3.5 (°K),
1e4<Re<2e6]
Coefficient H
H = 0.4 ..... T<Ts
H = 0.3 ..... T>Ts
Coefficient K
K = 1.27 - 0.27 * (Ts/Tdef) ..... [0.5<Ts/Tdef<1, Ts(°K),
T(°K)]
K = (Ts/Tdef)^(-0.55) ..... [1<Ts/Tdef<3.5, Ts(°K),
T(°K)]
Coefficient E
| ▼ Re... L/D ► | 1 | 2 | 5 | 10 | 15 | 20 | 30 | 40 | 50 | 1000 |
| 1.00E+04 | 1.65 | 1.50 | 1.34 | 1.23 | 1.17 | 1.13 | 1.07 | 1.03 | 1.00 | 1.00 |
| 2.00E+04 | 1.51 | 1.40 | 1.27 | 1.18 | 1.13 | 1.10 | 1.05 | 1.02 | 1.00 | 1.00 |
| 5.00E+04 | 1.34 | 1.27 | 1.18 | 1.13 | 1.10 | 1.08 | 1.04 | 1.02 | 1.00 | 1.00 |
| 1.00E+05 | 1.28 | 1.22 | 1.15 | 1.10 | 1.08 | 1.05 | 1.03 | 1.02 | 1.00 | 1.00 |
| 1.00E+06 | 1.14 | 1.11 | 1.08 | 1.05 | 1.04 | 1.03 | 1.02 | 1.01 | 1.00 | 1.00 |
| 1.00E+12 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
01b. Écoulement en conduite
- Section circulaire
(D,L) : [Tdef = (T+Ts)/2, 0.1<Re<1e7] ... (Principles of Heat Transfer
7th. edtion)
hc = (Nu *
λ) / D
Nu = (3.65 + (0.0668 * Re * Pr * (D/L)) / (1 + 0.045 * (Re * Pr *
(D/L))^(2/3))) * (μ / μs)^0.14 ..... [Re<2100]
Nu = 0.023
* Re^0.8
*
Pr^H ..... [0.5<Pr<160,
6000<Re<1e7, L/D<60]
Coefficient H
H = 0.4 .... T<Ts
H = 0.3 .... T>Ts
01c.
Écoulement en conduite - Section circulaire
(D,L) : [Tdef = (T+Ts)/2, 0.1<Re<1e7] ...
(Heat Transfer Applications for the Practicing Engineer)
hc = (Nu *
λ) / D
Nu = 1.86 * (Re * Pr * (D / L))^(1/3) * (μ / μs)^0.14
..... [Re<2100]
Nu =0.027 * Re^0.8 * Pr^(1/3) *
(μ / μs)^0.14 ..... [0.5
< Pr < 10000,
Re>2100]
Re-Nu graphique pour l'air et l'eau (T ... [°C], D,Dh,L ... [mm])

02. Écoulement en conduite
- Section rectangulaire (a,b) Dh = 2 * a * b / (a + b) : [Tdef =
(T+Ts)/2, 0.1<Re<1e7] ...
(Strojírenská příručka)
03. Écoulement en conduite - Section carrée (a) Dh = a : [Tdef = (T+Ts)/2, 0.1<Re<1e7]
...
(Strojírenská příručka)
04. Écoulement en conduite - Section hexagonale (a) Dh = a : [Tdef = (T+Ts)/2,
0.1<Re<1e7] ...
(Strojírenská příručka)
06. Écoulement en conduite - Section quelconque (Ac,P) Dh = 4 * Ac / P : [Tdef =
(T+Ts)/2, 0.1<Re<1e7] ...
(Strojírenská příručka)
hc = (Nu *
λ) / Dh
Nu = (3.65 + (0.0668 * Re * Pr * (Dh/L)) / (1 + 0.045 * (Re * Pr *
(Dh/L))^(2/3))) * (μ / μs)^0.14 .... [Re<2300]
Nu = 0.037*(1 + (Dh/L)^(2/3)) * (Re^0.75 - 180) * Pr^0.42 .... [Re>2300]
05. Écoulement en conduite - Cercle intermédiaire (d1,d2) Dh = d1 - d2 : [Tdef = (T+Ts)/2, 0.1<Re<1e7] ... (Gnielinski)
hc = (Nu * λ) / Dh
Écoulement laminaire [Re<2300] par approximation à partir du tableau :
| Rapport de diamètre | NuL1 | NuL2 |
| d2/d1 | (inside) | (outside) |
| 0.00 (tube) | - | 4.36 |
| 0.05 | 17.46 | 4.79 |
| 0.1 | 11.56 | 4.86 |
| 0.25 | 8.24 | 5.1 |
| 0.5 | 6.49 | 5.47 |
| 1.00 (planar slot) | 5.39 | 5.39 |
Écoulement turbulent [Re>4000] :
Pour le cercle restreint
NuT1=(0.86*(y)^(-0.16)) * NuS1
Pour le cercle extérieur
NuT2=(1 - ((1 - 0.86*(y)^0.16) / (3 * (y)))) * NuS2
y = d2 / d1 ... Rapport des diamètres
NuS = ((f / 8) * (Re - 1000) * Pr) / (1 + 12.7 * (f / 8)^0.5 * (Pr^(2/3) - 1))
f = (1.82 * log(Re) - 1.64)^(-2)
Courant dans la région de transition
(2300<Re<4000)
:
Interpolation linéaire à partir de NuL
et NuT
NuP = (1 - (Re - 2300)/1700) * NuL + ((Re - 2300)/1700) * NuT
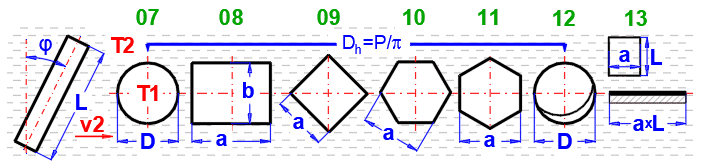
fcoeff ... Écoulement oblique autour d'un tube
| φ | 0° | 10° | 20° | 30° | 40° | 50° | 60° | 70° |
| fcoeff | 1.00 | 1.00 | 0.99 | 0.95 | 0.86 | 0.75 | 0.63 | 0.50 |
07a.
Écoulement autour d'un cylindre (D) : [Tdef = (T+Ts)/2, 0.5<Pr<1e3, 0.4<Re<4e5] ...
(Strojírenská příručka)
hc = (Nu *
λ) / D
* fcoeff
Nu =1.11 * K * Re^m * Pr^0.31
Nu =1.11 * K * Re^m * Pr^0.31 * (0.785 * (Ts/T)^(m/4) ..... for Gas
| Re | K | m |
| 0.4<Re<4 | 0.891 | 0.33 |
| 4<Re<40 | 0.821 | 0.385 |
| 40<Re<4e3 | 0.615 | 0.466 |
| 4e3<Re<4e4 | 0.174 | 0.618 |
| 4e4<Re<4e5 | 0.0239 | 0.805 |
07b.
Écoulement autour d'un cylindre (D) : [Tdef =
T, 0.5<Pr<1e3,
0<Re<1e6] ...
(Principles of Heat Transfer
7th. edtion)
hc = (Nu *
λ) / D
* fcoeff
Nu =C * Re^m * Pr^n * (Pr/Prs)^0.25
n = 0.37 [Pr<10]
n= 0.36 [Pr>10]
| Re | C | m |
| Re<40 | 0.75 | 0.4 |
| 40<Re<1e3 | 0.51 | 0.5 |
| 1e3<Re<2e5 | 0.26 | 0.6 |
| 2e5<Re<1e6 | 0.076 | 0.7 |
07c.
Écoulement autour d'un cylindre
(D) : [Tdef = (T+Ts)/2, 0.5<Pr<1e3, 0.04<Re<4e5] ...
(Heat Transfer Applications
for the Practicing Engineer)
hc = (Nu *
λ) / D
* fcoeff
Nu = C * Re^m * Pr^0.3333
| Re | C | m |
| 0.04<Re<4 | 0.989 | 0.33 |
| 4<Re<40 | 0.911 | 0.385 |
| 40<Re<4e3 | 0.683 | 0.466 |
| 4e3<Re<4e4 | 0.193 | 0.618 |
| 4e4<Re<4e5 | 0.027 | 0.805 |
Re-Nu graphique pour l'air et
l'eau (T
... [°C], D,Dh,L ... [mm])
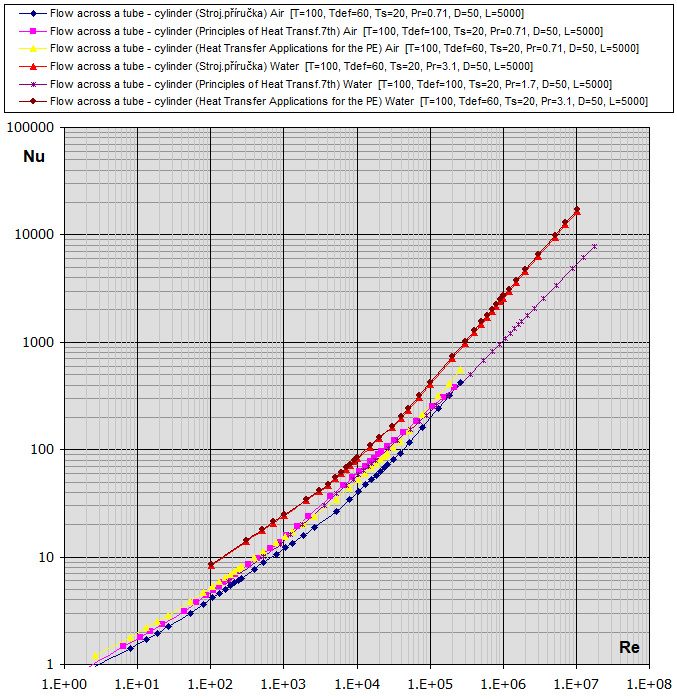

fcoeff ... Écoulement oblique autour d'un tube
| φ | 0° | 10° | 20° | 30° | 40° | 50° | 60° | 70° |
| fcoeff | 1.00 | 1.00 | 0.99 | 0.95 | 0.86 | 0.75 | 0.63 | 0.50 |
08a. Écoulement autour d'un tube à
section carrée (a) :
[Tdef = (T+Ts)/2, 5e3<Re<1e5,
0.5<Pr<1e3, 20<T<1000C] ...
(Strojírenská příručka)
Dh =4
* a / 3.14
Re = (Dh * v) / KinVis
hc = (Nu *
λ) / Dh
* fcoeff
Nu =1.11 *
0.0921 * Re^0.675 * Pr^0.31
Nu =1.11 * 0.0921 * Re^0.675 * Pr^0.31 * (0.785 * (Ts/T)^(0.675/4) ..... for Gas
08b. Écoulement autour d'un tube à
section carrée (a) :
[Tdef = T, 2.5e3<Re<1e5,
0.6<Pr<0.85] ...
(Principles of Heat Transfer
7th. edtion)
Dh = a
Re =(a * v) / KinVis
hc = (Nu *
λ)
/ a
* fcoeff
Nu =
0.16
*
Re^0.699
... [2.5e3<Re<8e3]
Nu = 0.092 * Re^0.675 ... [5e3<Re<1e5]
08c. Écoulement autour d'un tube à
section rectangulaire (a,b) :
[Tdef
= (T+Ts)/2, 2.5e3<Re<1e5, 0.5<Pr<1e3,
0.5<a/b<1] ...
(Principles of Heat Transfer
7th. edtion)
Dh =2
* (a + b) / 3.14
Re = (Dh * v) / KinVis
hc = (Nu *
λ)
/ a
* fcoeff
Nu = 0.104 *
Pr^0.35 * Re^0.675
..... [a/b=1]
Nu
= 0.264
* Pr^0.35 * Re^0.66
...... [a/b=0.5]
Re-Nu-hc graphique pour l'air et l'eau (T ... [°C], D,Dh,L ... [mm])
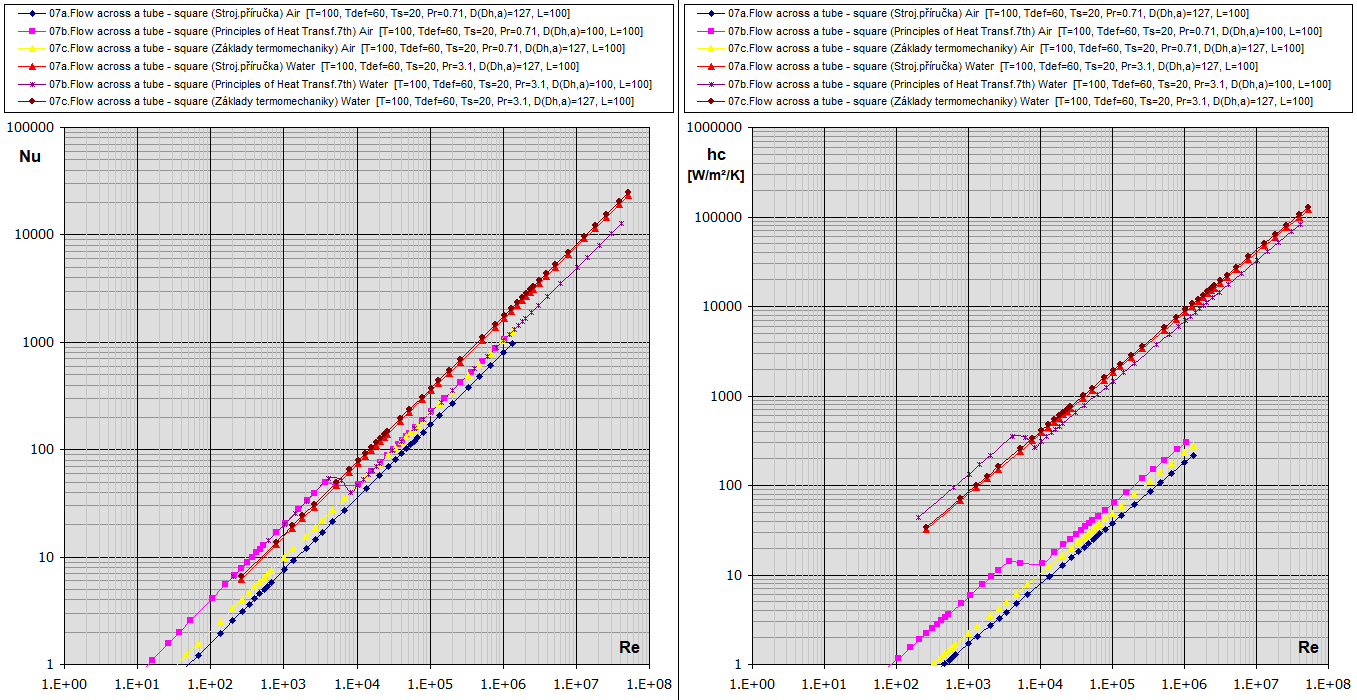
09a.
Écoulement autour d'un tube à section carrée (a):
[Tdef = (T+Ts)/2, 5e3<Re<1e5,
0.5<Pr<1e3, 20<T<1000C] ...
(Strojírenská příručka)
Dh =4 * a / 3.14
Re = (Dh * v) / KinVis
hc = (Nu *
λ) / Dh
* fcoeff
Nu =1.11 *
0.222 * Re^0.588 * Pr^0.31
Nu =1.11 * 0.222 * Re^0.588
* Pr^0.31 * (0.785 * (Ts/T)^(0.588/4) ..... for Gas
09b.
Écoulement autour d'un tube à section carrée (a) :
[Tdef = T, 2.5e3<Re<1e5,
0.6<Pr<0.85] ...
(Principles of Heat Transfer
7th. edtion)
x = (2 *
a^2)^0.5
Re =(x *
v) / KinVis
hc = (Nu *
λ)
/ x
* fcoeff
Nu =
0.261*
Re^0.624 ... [2.5e3<Re<7.5e3]
Nu = 0.222 * Re^0.588 ... [5e3<Re<1e5]
10a. Écoulement
autour d'un tube à section hexagonale (a) :
[Tdef = (T+Ts)/2, 5e3<Re<1e5,
0.5<Pr<1e3, 20<T<1000C] ...
(Strojírenská příručka)
Dh =6 * a / (3^0.5) / 3.14
Re = (Dh * v) / KinVis
hc = (Nu *
λ) / Dh
* fcoeff
Nu =1.11 *
0.138 * Re^0.638 * Pr^0.31
Nu =1.11 * 0.138 * Re^0.638
* Pr^0.31 * (0.785 * (Ts/T)^(0.638/4) ..... for Gas
10b. Écoulement autour d'un tube à
section hexagonale (a) :
[Tdef = (T+Ts)/2,
5e3<Re<1e5,
0.6<Pr<0.85] ... (Principles of Heat
Transfer
7th. edtion)
Re =(a *
v) / KinVis
hc = (Nu *
λ)
/ a
* fcoeff
Nu = 0.138 * Re^0.638
11a.
Écoulement autour d'un tube à section hexagonale (a) :
[Tdef = (T+Ts)/2, 5e3<Re<1.95e4,
0.5<Pr<1e3, 20<T<1000C] ...
(Strojírenská příručka)
Dh =6 * a / (3^0.5) / 3.14
Re = (Dh * v) / KinVis
hc = (Nu * λ) / Dh
* fcoeff
Nu =1.11 *
0.144
* Re^0.638 * Pr^0.31
Nu =1.11 * 0.144 * Re^0.638
* Pr^0.31 * (0.785 * (Ts/T)^(0.638/4) ..... for Gas
11b.
Écoulement autour d'un tube à section hexagonale (a) :
[Tdef = (T+Ts)/2, 5e3<Re<1e5, ,
0.6<Pr<0.85] ... (Principles of Heat
Transfer
7th. edtion)
x = 2 * a /
(3^0.5)
Re =(x *
v) / KinVis
hc = (Nu *
λ)
/ x
* fcoeff
Nu =
0.144
*
Re^0.638 ... [5e3<Re<1.95e4]
Nu = 0.035 * Re^0.782 ... [1.95e4<Re<1e5]
12.
Écoulement autour d'une sphère (D) :
[Tdef = T, 3.5<Re<2e5,
0.7<Pr<380] ... (Principles
of Heat Transfer
7th. edtion)
hc = (Nu *
λ)
/ D * fcoeff
Nu =2 + (0.4 *
Re^0.5 + 0.06 * Re^(0.67)) * Pr^0.4 * (μ
/ μs)^0.25 ...
[3.5<Re<76000]
Nu =2 + (Re / 4 + 0.0003 *Re2^1.6)^0.5 ... [76000<Re<2e5]
13.
Enroulement des plaques φ=90° (a) : [Tdef
= (T+Ts)/2, Re<1e7, 0.6<Pr<60]
... (Heat
Transfer Applications for the Practicing Engineer)
Re =(a *
v) / KinVis
hc = (Nu *
λ)
/ a
* fcoeff
Nu =
0.644
*
Re^0.5 *
Pr^0.333
... [Re<5e5,
0.6<Pr<50]
Nu = 0.037 * Re^0.8 * Pr^0.333 ... [5e5<Re<1e7,
0.6<Pr<60]
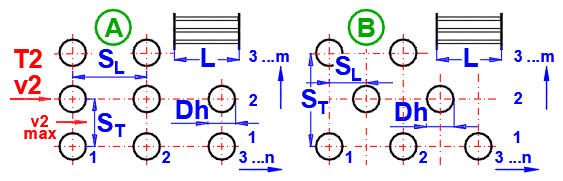
A.
Écoulement autour d'un faisceau de tubes (D,
ST, SL, n) : [Tdef = (T+Ts)/2, 0.7<Pr<500, 10<Re<200000]
...
(Principles of Heat Transfer
7th. edtion)
hc = (Nu *
λ) / D * A
Nu = 0.8 * Re^0.4 * Pr^0.36 * (Pr/Prs)^0.25 [10<Re<1000]
Nu = 0.27 * Re^0.63 * Pr^0.36 * (Pr/Prs)^0.25 [1000<Re<2e5, ST/SL>0.7]
Nu = 0.021 * Re^0.84 * Pr^0.36 * (Pr/Prs)^0.25 [2e5<Re]
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Coeff A |
0.68 |
0.75 |
0.83 |
0.89 |
0.92 |
0.95 |
0.97 |
0.98 |
0.99 |
1.00 |
|
Coeff B |
0.64 |
0.80 |
0.87 |
0.90 |
0.92 |
0.94 |
0.96 |
0.98 |
0.99 |
1.00 |
B.
Écoulement autour d'un faisceau de tubes (D,
ST, SL, n) : [Tdef = (T+Ts)/2, 0.7<Pr<500, 10<Re<200000]
...
(Principles of Heat Transfer
7th. edtion)
hc = (Nu *
λ) / D * B
Nu = 0.9 * Re^0.4 * Pr^0.36 * (Pr/Prs)^0.25 [10<Re<1000]
Nu = 0.35 * (ST/SL)^0.2 * Re^0.6 * Pr^0.36 * (Pr/Prs)^0.25 [(ST/SL)<2,
1000<Re<2e5]
Nu = 0.4 * Re^0.6 * Pr^0.36 * (Pr/Prs)^0.25 [(ST/SL)>2, 1000<Re<2e5]
Nu = 0.022 * Re^0.84 * Pr^0.36 * (Pr/Prs)^0.25 [Pr>1, 2e5<Re]
Nu = 0.019 * Re^0.84 [Pr=0.7, 2e5<Re]
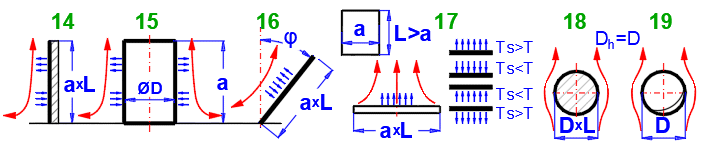
14-15.
Plaque verticale ou cylindre vertical
(L) : [Tdef = (T+Ts)/2, 1e3 < Ra < 1e13]
... (Heat Transfer Applications for the Practicing Engineer)
hc = (Nu *
λ)
/ L
Nu = 0.59 * Ra^0.25
[1e4<Ra<1e9]
Nu = 0.10 * Ra^0.333 [1e9<Ra<1e13]
16. Plaque inclinée
(L) :
[0°<φ<89.9°, Tdef = (T+Ts)/2, 1e3 < Ra < 1e13]
...
(Principles of Heat Transfer
7th. edtion)
hc = (Nu *
λ)
/ L
Nu = 0.59 * (Ra*cos(φ))^0.25
[1e4<Ra<1e9]
Nu = 0.10 * (Ra*cos(φ))^0.333
[1e9<Ra<1e13]
17.
Plaque - Face supérieure (plus petite
dimension A x B)
: [Tdef = (T+Ts)/2, 2e4 < Ra < 1e11]
... (Heat Transfer Applications for the Practicing Engineer)
hc = (Nu *
λ)
/ L
Ts > T
Nu = 0.54 * Ra^0.25 [2e4 < Ra < 8e6]
Nu = 0.15 * Ra^0.333 [8e6 < Ra < 1e11]
Ts < T
Nu = 0.58 * Ra^0.2 [8e6 < Ra < 1e11]
17.
Plaque - Face inférieure (plus petite
dimension A x B)
: [Tdef = (T+Ts)/2, 2e4 < Ra < 1e11]
... (Heat Transfer Applications for the Practicing Engineer)
hc = (Nu *
λ)
/ L
Ts < T
Nu = 0.54 * Ra^0.25 [2e4 < Ra < 8e6]
Nu = 0.15 * Ra^0.333 [8e6 < Ra < 1e11]
Ts > T
Nu = 0.58 * Ra^0.2 [8e6 < Ra < 1e11]
18.
Cylindre horizontal (D) : [Tdef
= (T+Ts)/2, 1e-5 < Ra < 1e12] ...
(Heat Transfer Applications for the Practicing Engineer)
hc = (Nu *
λ)
/ D
Nu = 0.4 * Ra^0 [0 < Ra < 1e-5]
Nu = 0.85 * Ra^0.188 [1e-5 < Ra < 1e4]
Nu = 0.53 * Ra^0.25 [1e4 < Ra < 1e9]
Nu = 0.13 * Ra^0.333 [1e9 < Ra < 1e12]
19. Sphère (D) : [Tdef = (T+Ts)/2, 1e-5 < Ra < 1e12]
... (Heat Transfer Applications for the Practicing Engineer)
hc = (Nu *
λ)
/ D
Nu1=0.6 * Ra^0.25
Nu2=2 + (0.589 * Ra^0.25) / (1 + (0.469 / Gr^(9/16)))^(4/9)
Nu=(Nu1 + Nu2) / 2
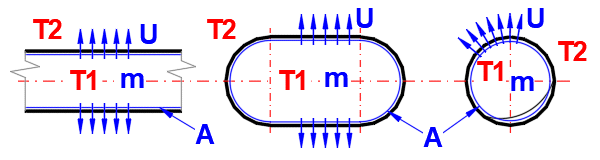
L'ailetage est utilisé pour augmenter le transfert de chaleur (en augmentant la surface d'échange thermique) dans diverses applications telles que les dissipateurs thermiques d'ordinateurs, les systèmes de chauffage et les échangeurs de chaleur. La méthode de calcul la plus simple (et approximative) ne prend en compte que la surface totale de la surface ailetée et le coefficient de transfert de chaleur hc rapporté à la surface non ailetée.
Les équations utilisées dans ce calcul tiennent également compte d'autres paramètres, tels que la forme et les dimensions de l'ailette.
Le calcul de l'ailetage
donne la surface totale d'échange thermique At
et l'efficacité globale de l'ailetage ηof.
L'équation modifiée pour le calcul du flux thermique convectif spécifique qc′
est :
qc' = hc * (T - Ts) * ηof
Et pour le calcul du flux thermique convectif total Qc, l'équation est :
Qc = qc' * At
Les formes d'ailettes et les conditions d'écoulement autour des ailettes traitées dans cette application sont décrites ci-dessous.
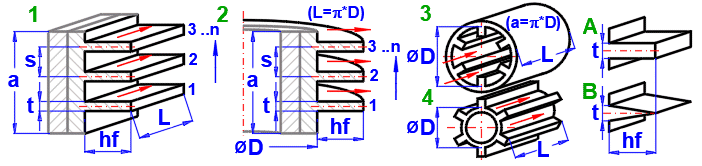
1A) Ailettes Droites - Rectangulaires
Af = 2 * hfc * L [m²]
hfc = hf + (t/2) [m]
Ap = t * hf [m²]
1B) Ailettes Droites - Triangulaires
Af = 2 * L * (hf^2 + (t/2)^2)^0.5 [m²]
Ap = (t /2) * hf
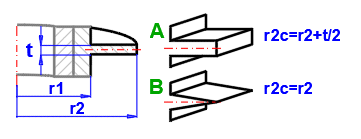
2A) Ailettes Annulaires - Rectangulaires
Af = (3.1416 * (D/2 + hfc)^2 - 3.1416 * (D/2)^2) * 2
hfc = hf + (t/2) [m]
Ap = t * hf [m²]
2B) Ailettes Annulaires - Triangulaires
Af = (3.1416 * (D/2 + hfc)^2 - 3.1416 * (D/2)^2) * 2
hfc = (hf^2 + (t / 2.3)^2)^0.5)
Ap = (t /2) * hf
Où :
Af
... Surface de l'ailette
hf
... Hauteur de l'ailette
hfc
... Hauteur corrigée de l'ailette
Ap
... Surface de la section transversale de l'ailette
La coordonnée x du graphique est une
valeur sans dimension :
x = hfc^(3/2) * (hc / (Lambda * Ap))^(1/2)
hc
... Coefficient de transfert de chaleur [W/m²K]
Lambda ... Conductivité thermique du matériau de l'ailette [W/(m.K)]
La coordonnée y du graphique est l'efficacité de l'ailette ηf.
Efficacité des ailettes droites à profil rectangulaire, triangulaire et parabolique
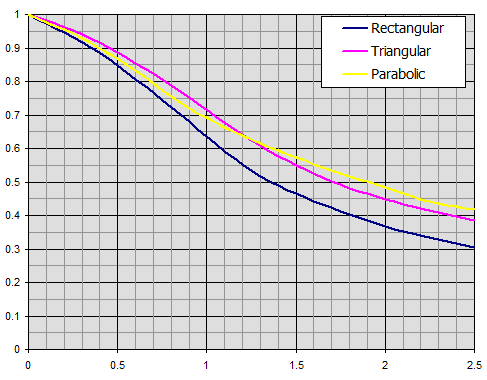
Efficacité des ailettes annulaires d'épaisseur constante t
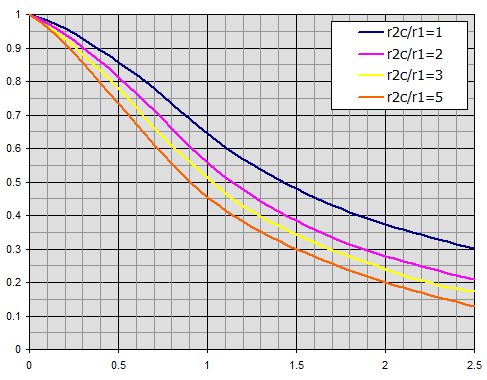
Les courbes individuelles se rapportent au rapport des rayons r2c/r1.
ηof = (1 - (n * Af) / At * (1 - ηf))
Où :
n ... Nombre d'ailettes
Af
... Surface de l'ailette
At
... Surface totale
ηf
... Efficacité de l'ailette
L'énergie radiante est transférée par rayonnement électromagnétique de différentes longueurs d'onde. La problématique du transfert de chaleur par rayonnement est assez complexe ; c'est pourquoi seules les tâches fondamentales couramment utilisées dans la pratique de l'ingénierie mécanique sont abordées ici.

Dans les formules, la notation est utilisée conformément à l'illustration.
hr = ɛ * δ0 * (Ts^4 - Tsky^4) / (Ts - Tsky)
Où:
ε ... Émissivité de la paroi [0...1]
δ0 ... Constante de Stefan-Boltzmann, δ0=5.67e-8
[W/m²/K⁴]
Ts
... Température de la paroi [°K]
Tsky
... Température de l'espace [°K]
Q1 = ε1 * δ0 * A1 * (T1K^4 - Tsky^4)
Où:
ε1 ... Émissivité de la paroi [0...1]
δ0 ... Constante de Stefan-Boltzmann,
δ0 = 5.67e-8
[W/m²/K⁴]
Tsky
... Température de l'espace [°K]
T1K ... Température de la paroi [°K]
q1 = Q1 / A1
A1 ... Surface de la paroi [m²]
Q12 = (δ0 * A1 * (T1K^4 - T2K^4)) / (1/ε1 + A1/A2 * (1/ε2 - 1))
Où:
ε1 ... Émissivité de la paroi 1 [0...1]
ε2 ... Émissivité de la paroi 2 [0...1]
A1 ... Surface de la paroi 1 [m²]
A2 ... Surface de la paroi 2 [m²]
T1K ... Température de la paroi 1 [°K]
T2K ... Température de la paroi 2 [°K]
q12 = Q12 / A1
A1 ... Surface de la paroi 1 [m²]
Q12 =(δ0 * (T1K^4 - T2K^4)) / ((1 - ε1) / (ε1 * A1) + (1 - ε3) / (ε3 * Ax) + (1 - ε4) / (ε4 * Ax) + (1 - ε2) / (ε2 * A2))
Où:
ε3 ... Émissivité de l'écran de protection x [0...1]
ε4 ... Émissivité de l'écran de protection x [0...1]
Ax
... Surface de l'écran de protection x [m²]
q12 = Q12 / A1
A1 ... Surface de la paroi 1 [m²]
Tx = ((R1 * T2K^4 + R2 * T1K^4) / (R1 + R2))^0.25
Où:
R1 ... Résistance entre 1 et x
R2 ... Résistance entre x et 2
R1 = (1 - ε1) / (ε1 * A1) + (1-ε3) / (ε3 * Ax)
R2 = (1 - ε4) / (ε4 * Ax) + (1 - ε2) / (ε2 * A2)
Q12 = (δ0 * (T1K^4 - T2K^4)) / Rsum
Rsum = R1 + R2 + R3
R1 = (1 - ε1) / (ε1 * A1) + (1 - ε3) / (ε3 * Ax)
R2 = (1 - ε4) / (ε4 * Ax) + (1 - ε5) / (ε5 * Ay)
R3 =(1 - ε6) / (ε6 * Ay) + (1 - ε2) / (ε2 * A2)
R1 ... Résistance entre 1 et x
R2 ... Résistance entre x et y
R3 ... Résistance entre y et 2
q12 = Q12 / A1
A1 ... A1 ... Surface de la paroi 1 [m²]
Tx = (T1K^4 - Q12 * R1 / δ0)^0.25
Ty = (T2K^4 + Q12 * R3 / δ0)^0.25
Le calcul du flux thermique composite n'est pas simple et ne peut pas être résolu directement. Le flux thermique dépend d'une multitude de paramètres (températures, propriétés du fluide, matériau de la paroi, géométrie, etc.) qui varient avec la température de la paroi.
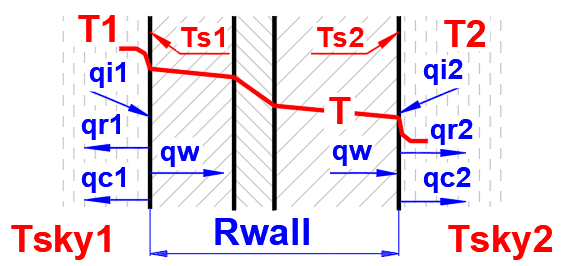
Pour déterminer les
températures de paroi Ts1 et Ts2, l'équation du flux thermique est appliquée en
utilisant les paramètres spécifiés du fluide et de la paroi. Les températures
Ts1 et Ts2 sont progressivement affinées pour satisfaire les équations suivantes
:
Ts2 = Ts1 - q1 * Rwall, Q1 = -Q2
Q1 = (qi1 + qr1 + qc1) * A1
Q2 = (qi2 + qr2 + qc2) * A2
Q1 ... Flux thermique total du côté
gauche [W]
Q2 ... Flux thermique total du côté droit [W]
Les relations
suivantes (voir sections précédentes) sont utilisées pour calculer le flux
thermique q :
qc = hc * (T - Ts) ... f (T, Ts, p, Rho, μ, Cp, λ.....)
qr = hr * (T - Ts) ... f (T, Ts, ε.....)
qi ... Paramètre d'entrée -
irradiation directe (soleil, source de chaleur externe, etc.)
La résolution des températures de paroi Ts1 et Ts2 entraînera, bien entendu, une modification des valeurs de hc1, hc2, hr1 et hr2. Par conséquent, une deuxième itération peut être lancée manuellement, où les nouvelles valeurs de hc1 et hc2 sont utilisées à plusieurs reprises pour affiner davantage les résultats.
Résolution des températures Ts1 et Ts2 :
Première
estimation (n=1) :
Ts1K[°K] = 100
*
(ABS((T1K
/
100)^4 - qi1
/ c0'))^0.25
Ts2K[°K] =
Ts1K - q1 * Rwall
qc1[W/m²] =
(T1K
-
Ts1K)
*
hc1
*
FinEff1
qc2[W/m²] = (Ts2K - T2K) * hc2
*
FinEff2
qr1[W/m²] =
(Tsky1
-
Ts1K)
*
hr1
qr2[W/m²] = (Ts2K - Tsky2) * hr2
q1[W/m²] = qi1 + qc1 + qr1
q2[W/m²] = qi2 + qc2 + qr2
ΔQ[W] =
Q1
-
Q2 = (q1 * A1 - q2 * A2) /
A2
ΔTs2 =IF(ABS(ΔQ)
> 1;(ΔQ/ABS(ΔQ)*(ABS(ΔQ)^0.5));ΔQ/2)
Approximation (100 étapes, méthode de
la bissection, n=2…100) :
Ts1K(n) = Ts1K(n-1) + ΔTs2(n-1)
Ts2K(n) = Ts1K(n) - q1 * Rwall
qc1(n) = (T1K
-
Ts1K(n))
*
hc1
*
FinEff1
qc2(n) = (Ts2K(n) - T2K) * hc2
*
FinEff2
qr1 =
(Tsky1
-
Ts1K(n))
*
hr1
qr2 = (Ts2K(n) - Tsky2) *
hr2
qw(n) =
1
/
Rwall
*
(Ts2K(n)
- Ts1K(n))
q1(n) = qi1 + qc1(n) + qr1(n)
q2(n) = qi2 + qc2(n) + qr2(n)
ΔQ(n) =
Q1(n)
-
Q2(n) = (q1(n) * A1 - q2(n)
* A2) / A2
ΔTs2(n) = IF(ΔQ(n-1)*ΔQ(n) < 0; ΔTs2(n-1)/-2; ΔTs2(n-1))
Où :
c0′=δ0 * 1e8=5.67
δ0=5.67e-8 ... Constante de Stefan-Boltzmann
[W/m²/K⁴]
Rwall ... Résistance thermique de la paroi
[m²K/W]
Tsky
... Température ambiante de l'espace
[°K]
FinEff
... Efficacité des ailettes [0 ... 1]
Pour déterminer avec précision le changement de température longitudinal dans une tuyauterie avec un fluide en circulation (liquide, gaz), l'équation suivante s'applique :
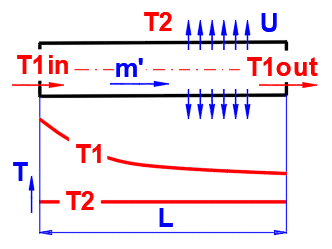
dTL = ABS(T1in - T2) * EXP(-Alpha * L)
T1in ... Température du
fluide à l'entrée [°C]
T2 ... Température ambiante [°C]
L ... Distance depuis l'entrée [m]
Alpha = U / (m' * Cp)
U ... Coefficient de
transfert de chaleur linéaire [W/m/K]
m′ ... Débit massique du fluide [kg/s]
Cp ... Capacité thermique massique du fluide [J/kg/K]
T1out =
T2 + dTL ...
(T1in>T2)
T1out = T2 - dTL .... (T1in<T2)
T1out ... Température de sortie (température à la distance L de l'entrée) [°C]
Puissance / Charge Thermique
Pw = -m' * Cp * (T1in - T1out) [W]
Le calcul du temps de refroidissement ne tient pas compte des changements de phase de la substance.
Phi = U * A * (1Ts - T2)
U ... Coefficient global de
transfert de chaleur [W/m²/K]
A ... Surface interne du tuyau, du réservoir [m²]
T1s ... Température initiale du fluide à l'intérieur [°C]
T2 ... Température ambiante [°C]
Time = ((T1s - T2) * m * Cp * LN((T1s - T2) / (T1e - T2)) / Phi
m ... Masse du fluide [kg]
Cp ... Capacité thermique massique du fluide [J/kg/K]
T1e ... Température finale du fluide à l'intérieur [°C]
Types de base d'échangeurs de chaleur
- Échangeur de chaleur à co-courant
- Échangeur de chaleur à contre-courant
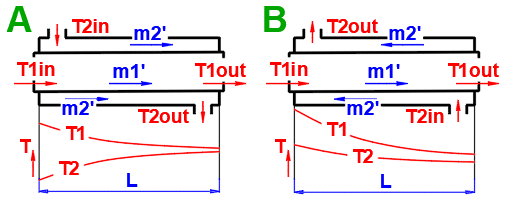
Types d'échangeurs de chaleur dérivés
Q1 = m1'
*
Cp1
*
dT1
Q2 = m2'
*
Cp2
*
dT2
Où:
m1', m2' ... Débit massique [kg/s]
Cp1, Cp2 ... Capacité thermique massique [J/kg/°K]
dT1, dT2 ... Différence de température [°C]
- Échangeur de chaleur à co-courant
- Échangeur de chaleur à contre-courant
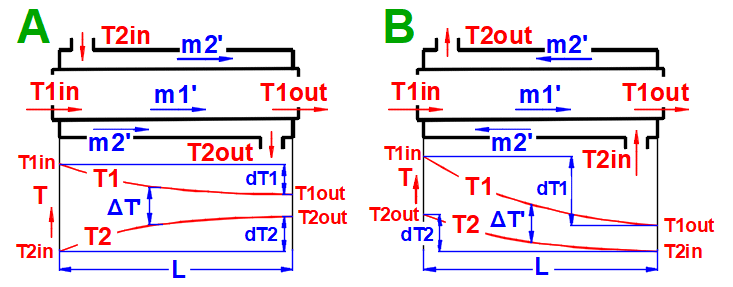
dT1 = T1Kout - T1Kin [°C]
dT2 = T2Kout - T2Kin [°C]
Co-courant A:
ΔTS' = ((T1Kin - T2Kin) - (T1Kout - T2Kout)) / (LN((T1Kin
- T2Kin) / (T1Kout - T2Kout)))
Contre-courant B:
ΔTP' = ((T1Kin - T2Kout) - (T1Kout - T2Kin)) /
(LN((T1Kin - T2Kout) / (T1Kout - T2Kin)))
Échangeur de type C-H: ΔTX' = ΔTP' * Epsilon
Où:
T1Kin, T2Kin ...
Température d'entrée du fluide [°K]
T1Kout, T2Kout ... Température de sortie du fluide [°K]
Epsilon ... Facteur de correction pour la différence de température moyenne
logarithmique [0.5 -
1.0]
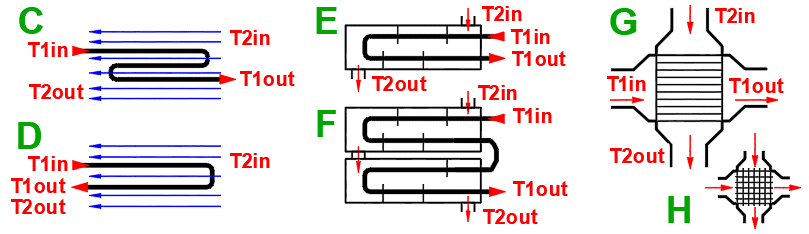
Le facteur de correction est approximé à partir de tableaux en utilisant l'interpolation linéaire pour les échangeurs de type C-H.
Rapport des capacités thermiques R
R = (T1Kin - T1Kout) / (T2Kout - T2Kin)
Efficacité thermique P
P = (T2Kout - T2Kin) / (T1Kin - T2Kin)
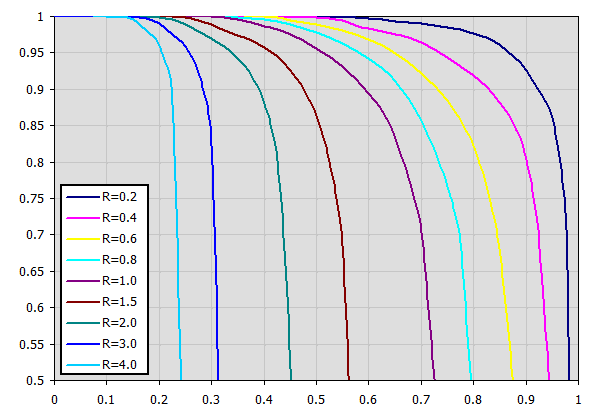
Les graphiques correspondants pour Epsilon pour de nombreux types d'échangeurs sont disponibles dans la littérature citée.
Exemple de graphique (approximation de tableau) pour l'échangeur de type F: (Xaxe ... P, Yaxe ... Epsilon) Pour P=0.7, R=0.8 => Epsilon=0.85
A = ABS(Q1 / (Upl * ΔT'))
Où:
Q1,Q2 ... Flux de chaleur [W], condition: Q1=−Q2
ΔT' ... Différence de température moyenne logarithmique (ΔTS',
ΔTP', ΔTX') [°C]
Upl ...
Coefficient global de transfert de chaleur - paroi plane [W/m²/K]
L = ABS(Q1 / (Ucyl * ΔT'))
Où:
Q1,Q2 ... Flux de chaleur [W], condition: Q1=−Q2
ΔT' ... Différence de température moyenne logarithmique (ΔTS',
ΔTP', ΔTX') [°C]
Ucyl ...
Coefficient global de transfert de chaleur - paroi cylindrique [W/m/K]
Co-courant A: T1Out = T1in - Theta1S
Contre-courant B: T1Out = T1in - Theta1P
Échangeur de type C-H:
T1Out =
T1in - Theta1X
Co-courant A: T2Out = T2in + Theta2S
Contre-courant B: T2Out = T2in + Theta2P
Échangeur de type C-H:
T2Out =
T2in - Theta2X
Theta1S = (T1Kin - T2Kin) * FiS
Theta1P = (T1Kin - T2Kin) * FiP
Theta1X = (T1Kin - T2Kin) * FiX
Theta2S = C1 / C2 * Theta1S
Theta2P = C1 / C2 * Theta1P
Theta2X = C1 / C2 * Theta1X
C1 = m1'
*
Cp1
C2 = m2'
*
Cp2
Co-courant A: FiS = (1 - EXP(-U * OmegaS * LA)) / (1 + C1/C2)
Contre-courant B: FiP = (1 - EXP(-U * OmegaP * LA)) / (1 - C1/C2 * EXP(-U * OmegaP *
LA))
Échangeur de type C-H:
FiX =
(1 - EXP(-U * OmegaX * LA)) / (1 - C1/C2 * EXP(-U * OmegaX * LA))
LA = Areq / (1 / Epsilon)
Areq ...
Surface spécifiée pour laquelle la température de sortie doit être déterminée [m²]
Epsilon ... Facteur
de correction pour la différence de température moyenne logarithmique (Échangeur
de type C-G) [0.5 - 1.0]
U ... Coefficient global de transfert de chaleur - paroi plane [W/m²/K]
Co-courant A: OmegaS = 1/C1 + 1/C2
Contre-courant B:
OmegaP =1/C1 - 1/C2
Échangeur de type C-H: OmegaX =1/C1 - 1/C2
Rf = 1/Ud - 1/Uc
Ud = 1/ (Rf + 1/Uc)
Où:
Rf ... Facteur d'encrassement [m²K/W]
Uc ... Coefficient global de transfert de chaleur pour surface propre [W/m²/K]
Un grand nombre de constructions techniques (bâtiments) sont exposées au rayonnement solaire. Ce calcul sert à déterminer le flux thermique solaire par unité de surface pour des conditions données (orientation de la surface, date, heure, altitude, pollution) et à déterminer l'apport énergétique journalier total.
Relations Utilisées
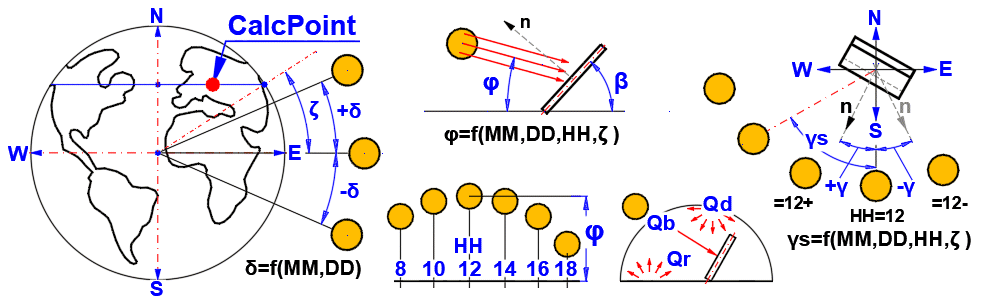
Angles :
δ = 23.45 * SIN((360 * (284 + nn) / 365) * PI()/180)
nn ...
Jour séquentiel de l'année (1-365)
φ = ASIN((SIN(Latitude*PI()/180) * SIN(δ*PI()/180)) + (COS(Latitude*PI()/180) * COS(δ*PI()/180) * COS(15*PI()/180*(HH-12))))*180/PI()
Latitude ... Latitude géographique [deg]
HH ...
Heure [0-24]
γs = ASIN(COS(δ*PI()/180) / COS(φ*PI()/180) * SIN(Tau*PI()/180))*180/PI()
Tau = 15 * (HH-12) ... Angle horaire solaire [deg] (matin (-), après-midi (+))
θ = ACOS((SIN(φ*PI()/180) * COS(β*PI()/180) + COS(φ*PI()/180) * SIN(β*PI()/180) * COS((γs - γ)*PI()/180)))*180/PI()
β ... Inclinaison de la surface (0-90) [deg]
γ ... Azimut de la surface (+-180) [deg]
Puissance de Rayonnement :
Qon =SolarConst * (1 + 0.033 * COS((360*nn/365)*PI()/180))
Le flux de rayonnement solaire en dehors
de l'atmosphère varie de ±3.3% au cours de l'année (distance Terre-Soleil).
SolarConst ...
Constante solaire (valeur moyenne 1367W/m²)
Qbn = Qon * EXP( -(Zcoeff / EpsilonCoeff))
Zcoeff ... Coefficient de pollution atmosphérique (1.5 -6)
EpsilonCoeff = (9.38076 * (SIN(φ*PI()/180) + (0.003 + SIN(φ*PI()/180)^2)^0.5)) /
(2.0015 * (1-Lv*10^-4))+0.91018
Lv ...
Altitude [m]
QbT = Qbn * COS(θ*PI()/180)
Qd = 0.33 * (Qon - Qbn) * SIN(φ*PI()/180)
QdT = ((1+COS(β*PI()/180))/2) * Qd
QrT = Rhog * ((1 - COS(β*PI()/180))/2) * (Qb + Qd)
Qb = QbT * SIN(φ*PI()/180) / COS(θ*PI()/180)
Rhog ...
Rapport entre la densité de flux de rayonnement solaire réfléchie et incidente
(0-1).
QT' = QbT + QdT + QrT
QT = As * QT'
As ... Surface totale irradiée
Q = QT * Efficiency / 100
Efficiency ... Efficacité de conversion du rayonnement solaire en énergie utilisable (0-100).
Pour le calcul de Pw, la valeur de Q est déterminée toutes les 30 minutes de t=0−24h. Ces valeurs sont ensuite additionnées pour obtenir la Pw totale.
Pw = Sum (Q(t) * 0.5) [t=0-24]
Les calculs présentés ici couvrent des problèmes fréquemment rencontrés dans le domaine de la thermomécanique. Étant donné que ces problèmes ne sont que vaguement liés, aucune procédure universelle n'est décrite ici. Les procédures varient en fonction du problème spécifique. Si votre tâche relève du champ d'application des problèmes traités, nous vous recommandons de consulter les exemples fournis dans la documentation d'aide. Pour chaque type de calcul, plusieurs exemples types sont généralement inclus pour vous familiariser avec la procédure spécifique.
Dans ce chapitre, vous définissez les unités de calcul.
Choisissez le système d'unités de calcul désiré sur la liste. Après changement d'unités, toutes les valeurs seront immédiatement corrigées.
Ecrire la valeur que vous voulez convertir dans la case d'insertion du côté gauche. Choisir les unités à convertir et les unités de conversion à droite.
Cette section couvre les calculs énergétiques de base, y compris le chauffage, le refroidissement, le changement de phase et la combustion. Sauf indication contraire, les coefficients dans les tableaux sont fournis pour une température de 20 C et une pression de 0.1 MPa.
Remarque : De ce point de vue, les calculs doivent être considérés comme simplifiés. Les calculs ne valident pas les données d'entrée illogiques.
L'énergie doit être ajoutée ou retirée pour chauffer ou refroidir une substance.
Sélectionnez le groupe de matériaux. Le pointeur dans le tableau des matériaux (ligne suivante) sera réglé sur le premier matériau du type correspondant.
Sélectionnez le matériau.
Ce sont des valeurs informatives et n'ont aucune influence sur le calcul.
La valeur de Cp pour le matériau sélectionné est affichée dans le champ vert. Vous pouvez entrer votre propre valeur en décochant le bouton.
Entrez la masse du matériau chauffé ou refroidi. Le commutateur à droite détermine quelle valeur doit être calculée.
Entrez le changement de température.
L'énergie dépensée pour le changement de température.
L'énergie doit être ajoutée ou retirée lors d'un changement de phase (solide → liquide → gaz).
Sélectionnez le matériau. La température de fusion [TM] et la température d'ébullition [TB] sont indiquées entre crochets.
Les valeurs de CpM et CpB du matériau sélectionné dans la liste se trouvent dans le champ vert. Vous pouvez entrer vos propres valeurs en décochant le bouton.
Entrez la masse du milieu. Si la case est cochée, la valeur du calcul précédent sera utilisée.
L'énergie dépensée ou gagnée lors du changement de phase.
La Chaleur de Combustion
(Pouvoir Calorifique Supérieur - PCS ou HHV) est la quantité de chaleur libérée lors de la combustion isobare d'1 mole d'un composé dans de l'oxygène gazeux pour former les produits d'oxydation finaux. Il est supposé que l'eau libérée par la combustion se condense et que l'énergie de la réaction chimique n'a pas besoin d'être réduite de sa chaleur latente.
Le Pouvoir Calorifique Inférieur
(PCI ou LHV) suppose que l'eau est à l'état gazeux à la fin de la réaction.
Par conséquent, la valeur du PCS est toujours supérieure ou égale à la valeur du PCI. L'égalité se produit lorsqu'aucune eau n'est formée lors de la combustion.
Sélectionnez le matériau brûlé dans la liste.
Pour le Pouvoir Calorifique Inférieur (PCI ou LHV), l'eau est supposée être à l'état gazeux à la fin de la réaction.
La valeur de la Chaleur de Combustion (PCS ou HHV) est précise pour la combustion de composés définis (H2, CH4O, etc.). Pour les combustibles contenant divers mélanges (charbon, produits pétroliers, gaz naturel, etc.), les valeurs typiques peuvent être inférieures ou supérieures à la valeur tabulée. L'écart estimé par rapport aux valeurs tabulées est indiqué dans le champ vert. Vous pouvez entrer votre propre valeur de PCS en décochant le bouton.
Entrez la masse du matériau brûlé.
Le rendement de combustion indique la quantité d'énergie du combustible transférée au fluide caloporteur.
Chaudières à gaz :
Chaudières à condensation : jusqu'à 98 %
Chaudières basse température : jusqu'à 89 %
Chaudières conventionnelles : jusqu'à 84 %
Chaudières à combustible solide :
Chaudières à gazéification de bois ou de granulés de bois : jusqu'à 92 %
Chaudières automatiques à charbon : 80 à 90 %
Chaudières à charbon et autres combustibles solides : plus de 70 %
L'énergie gagnée par la combustion du combustible.
Ce paragraphe couvre le tableau périodique des éléments, le calcul de la masse molaire et de la constante de Poisson pour les éléments, les composés et leurs mélanges. La deuxième partie concerne le calcul de l'état et du changement d'état d'un gaz parfait (pV=mrT).
Entrez la formule chimique brute du composé. Après avoir appuyé sur le bouton ">>", la formule est décomposée en éléments individuels et la liste correspondante est remplie ci-dessous. Si vous souhaitez résoudre un mélange de composés, séparez-les par un signe "+". Lors de la lecture de la formule, le numéro de séquence du composé (de l'élément) dans le mélange est ajouté dans la dernière colonne du tableau.
Exemples de composés : h2so4, H2O, cO2, C4H10O, C2H3ClO2
Exemples de mélanges :
Air : N2+O2+Ar+CO2
Alcool(40%)+Eau(60%) : C2H5OH+H2O
Les boutons "1-20", "21-40"... remplissent le tableau avec les éléments correspondants.
Les paramètres de l'élément sélectionné dans la liste sont affichés sur la ligne correspondante. Le bouton "Clear" efface les lignes 2 à 20.
Symbole de l'élément.
Nombre d'atomes.
Masse atomique.
Masse molaire.
Densité de l'élément.
Capacité thermique massique.
Capacité thermique massique de fusion (chaleur de fusion).
Capacité thermique massique d'ébullition (chaleur de vaporisation).
Conductivité thermique.
Température de fusion.
Température d'ébullition.
Numéro de séquence du composé. Pour calculer les paramètres du mélange, il est nécessaire de déterminer le numéro de séquence du composé. Les éléments individuels dans le composé doivent donc avoir le même numéro de séquence.
Dans le tableau précédent, vous pouvez définir des éléments et des composés individuels marqués d'un numéro de séquence. Dans ce tableau, après avoir entré la fraction massique du mélange, vous pouvez déterminer la masse molaire totale du mélange.
Pour les gaz parfaits, la constante de Poisson est déterminée par le nombre de degrés de liberté de la molécule donnée.
Masse molaire de l'élément ou du composé individuel.
Entrez la fraction massique de chaque composant du mélange. Si la case à cocher à droite est sélectionnée, les valeurs d'origine sont conservées lors du remplissage du mélange à partir de la formule [3.2]. Si la case est décochée, la même valeur est attribuée à chaque composant du mélange.
La cellule de somme rouge à la fin de la ligne signale que la somme n'est pas égale à 100%.
Masse molaire du mélange.
r = R / Msum
R ... Constante universelle des gaz parfaits (8314.46261815324 J/kmol/K)
Msum ... Masse molaire du gaz
Le rapport des capacités thermiques d'un gaz à pression constante et à volume constant κ=cp/cv.
Pour les gaz parfaits, la constante de Poisson peut être déterminée à partir du nombre de degrés de liberté de la molécule donnée.
Cliquez sur le bouton "▼M,κ▼" pour transférer les valeurs M et κ à
la définition du gaz ci-dessous.
Le calcul permet de résoudre l'état d'un gaz parfait (pV=mrT), son changement d'état et de déterminer les valeurs énergétiques correspondantes (entropie, enthalpie, chaleur, travail...). Après avoir sélectionné (ou défini les paramètres physiques de) le gaz de travail, vous pouvez déterminer ses paramètres de fonctionnement (masse m, pression p, volume V et température T) sur la base de l'équation d'état des gaz parfaits :
p * V = m * r * T
r = R / M
M = m / N
Où :
p ... Pression absolue [Pa]
V ... Volume [m^3]
m ... Masse [kg]
T ... Température [K]
R ... Constante universelle des gaz parfaits R=8314.46261815324 [J/kmol/K]
M ... Masse molaire du gaz [kg/kmol] (air 28.966 kg/kmol)
N ... Quantité de matière [kmol]
r ... Constante spécifique du gaz [J/kg/K] (air 287.0427 J/kg/K)
A ... Exemple d'un système thermodynamique simple, gaz parfait p⋅V=m⋅r⋅T.
B ... Les processus réversibles peuvent être décrits plus généralement comme des processus polytropiques, où la capacité thermique du système (fermé) est constante. Dans un processus polytropique, toutes les variables d'état (p, V, T) changent généralement. Pour un processus polytropique dans un gaz parfait, l'équation p⋅Vn=const. s'applique. Les courbes de changement pour différentes valeurs de n sont indiquées dans les diagrammes p-V et T-s.
C ... Cycle de Carnot. Exemple d'un moteur thermique idéal composé de deux processus isothermes et de deux processus adiabatiques.
D ... Courbes des changements d'état réversibles de base :
o n=0, p=const, Isobare, (dp=0,wt=0,q=Δh,w=Δh−Δu)
o n=1, T=const, Isotherme, (dT=0,Δu=Δh=0,q=w=wt)
o n=κ, s=const, Isentropique, (ds=0,q=0,w=−Δu,wt=−Δh)
o n=∞, v=const, Isochore, (dv=0,w=0,q=Δu,wt=Δu−Δh)
Sélectionnez le gaz de travail dans la liste. S'il n'est pas dans la liste, décochez la case à droite et entrez les valeurs de M, cp et κ.
Avec le changement de température, cp,cv,κ du gaz changent. Pour les gaz prédéfinis, vous pouvez définir une température de référence (de travail). Le champ vert affiche la valeur recommandée (moyenne des valeurs max/min de T1...T6).
Cliquez sur le bouton "◄" pour transférer la valeur recommandée dans la cellule d'entrée.
Si vous définissez les paramètres du gaz, entrez la valeur.
r = R / M
r .... constante spécifique du gaz (air 287.0427 J/kg/K)
R ... Constante universelle des gaz parfaits (8314.46261815324 J/kmol/K)
M ... Masse molaire du gaz (air 28.996 kg/kmol)
Si vous définissez les paramètres du gaz, entrez la valeur.
Le rapport des capacités thermiques d'un gaz à pression constante et à volume constant κ=cp/cv. Pour les gaz parfaits, la constante de Poisson peut être déterminée à partir du nombre de degrés de liberté de la molécule donnée.
Entrez la quantité de matière. La masse correspondante est affichée sur la ligne suivante.
En appuyant sur le bouton "◄ N1", la quantité de matière remplie est attribuée à la masse m1 (point 1).
En appuyant sur le bouton "m1▼", la valeur de la masse est déplacée vers le champ m1 (point 1).
État d'équilibre et changement d'état d'un gaz parfait (équation d'état). 6 points (i=1−6) sont disponibles. À chaque point, l'état d'équilibre du gaz peut être déterminé par ses variables d'état p(i), V(i), T(i). Pour les points 2 à 6, il est possible de déterminer comment le changement d'état s'est produit de l'état (i−1) à (i). Les changements d'état peuvent être observés dans les graphiques "p-V" et "T-s".
Détermination de l'état d'équilibre :
Entrez successivement les valeurs que vous connaissez dans les cellules blanches du point sélectionné. Dans les cellules vertes à droite, les valeurs nécessaires pour atteindre l'état d'équilibre (p⋅V=m⋅r⋅T) sont calculées en continu. Vous transférez la valeur suggérée dans la cellule blanche avec le bouton "◄". La satisfaction de l'équation est signalée par le texte "▼ =OK ▼". Si l'équation d'état n'est pas satisfaite, le texte "▼ Erreur ▼" est affiché.
Changements d'état :
Si vous définissez les paramètres du gaz au point 2 (3, 4...), vous pouvez déterminer les changements des valeurs énergétiques (entropie, enthalpie, chaleur, travail...) par rapport au point précédent.
Procédure recommandée 1 : Changement isobare (p=const), isochore (V=const), isotherme (T=const).
- Utilisez le bouton "►" pour transférer l'état (m,p,V,T) au point suivant. (Le bouton "►=" insère un lien vers le point précédent. Par exemple, p2 sera "=p1", V2 sera "=V1", etc. La couleur des cellules sera grise).
- Modifiez une valeur d'entrée. Immédiatement, les valeurs suggérées pour atteindre l'état d'équilibre sont dans la colonne verte.
- Avec le bouton "◄", transférez la suggestion sélectionnée dans la cellule d'entrée (blanche).
Procédure recommandée 2 : Processus polytropique - la capacité thermique du système (fermé) est constante. Dans un processus polytropique, toutes les variables d'état (p, V, T) changent généralement. Pour un processus polytropique dans un gaz parfait, l'équation p⋅Vn=const. s'applique.
- Utilisez le bouton "►" pour transférer l'état (m,p,V,T) au point suivant.
- Modifiez une seule valeur d'entrée (p ou V ou T).
- Entrez l'exposant polytropique n et appuyez sur le bouton "◄ Polytr.◄". Les cellules d'entrée sont remplies de valeurs pour atteindre le n requis.
Mélange de gaz - bouton "3 = Mix (1+2)"
Calcul des paramètres du gaz résultant du mélange de deux parties (1+2) avec des paramètres p,V,T différents.
m = m1 + m2
p = m / M * R * T / V
V = V1 + V2
T = (m1 * T1 + m2 * T2) / (m1 + m2)
Les processus réversibles peuvent être décrits plus généralement comme des processus polytropiques, où la capacité thermique du système (fermé) est constante. Dans un processus polytropique, toutes les variables d'état (p, V, T) changent généralement.
Pour un processus polytropique dans un gaz parfait, l'équation p⋅Vn=const. s'applique.
Entrez la valeur souhaitée de n pour la transition entre deux états (précédent et actuel) dans la cellule d'entrée. À droite de la cellule d'entrée, la valeur actuelle calculée à partir de p,V,T est affichée. Le menu déroulant contient des valeurs significatives et fréquemment utilisées.
- Utilisez le bouton "►" pour transférer l'état (m,p,V,T) du point précédent.
- Modifiez une seule valeur d'entrée (p ou V ou T).
- En appuyant sur le bouton "▲Polytr.▲", les cellules d'entrée sont remplies de valeurs pour atteindre le n requis.
Si n="?", les valeurs (m,p,V,T) sont identiques à celles du point précédent.
Pour les valeurs sélectionnées de n :
n=0, p=const, Isobare, (dp=0,wt=0,q=Δh,w=Δh−Δu)
n=1, T=const, Isotherme, (dT=0,Δu=Δh=0,q=w=wt)
n=κ, s=const, Isentropique, (ds=0,q=0,w=−Δu,wt=−Δh)
n=∞, v=const, Isochore, (dv=0,w=0,q=Δu,wt=Δu−Δh)
n=ln(p2/p1)/(ln(p2/p1)−ln(T2/T1))
n=(ln(V2/V1)−ln(T2/T1))/ln(V2/V1)
Valeurs typiques de l'exposant polytropique :
Compresseur à piston : n=1.2–1.3 Processus avec dissipation thermique partielle, valeur typique pour les compresseurs lents avec refroidissement.
Compresseur axial : n=1.35–1.4 Turbo-compresseurs à grande vitesse avec une dissipation thermique minimale, plus proches d'un processus adiabatique (γ≈1.4 pour l'air).
Moteur à essence 4 temps (compression) : n=1.3–1.35 Compression du mélange de carburant avec dissipation thermique partielle dans les parois du cylindre.
Moteur diesel 4 temps (compression) : n=1.35–1.4 Rapport de compression plus élevé et compression d'air pur, pertes thermiques moindres que pour un moteur à essence.
La ligne indique la capacité thermique massique polytropique et l'état du gaz :
- "▼ =OK ▼". L'état d'équilibre est atteint.
- "▼ Erreur ▼". Si l'état d'équilibre n'est pas atteint.
Si cn="?", les valeurs (m,p,V,T) sont identiques à celles du point précédent.
Le bouton "►►" copie les valeurs (m1,p1,V1,T1) dans tous les autres points.
Entrez la masse du fluide de travail. Si le chiffre d'entrée est rouge, c'est seulement un avertissement que la valeur de m dans le point précédent est différente. Cela ne doit pas nécessairement être une erreur !
Entrez la pression absolue du fluide de travail.
Entrez le volume du fluide de travail.
Entrez la température du fluide de travail.
Valeurs pour les points individuels (états) dans un seul tableau.
Entropie
S1 = (cv * LN(T1) + r * LN(V1)) * m1
S2 = (cv * LN(T2) + r * LN(V2)) * m2
Le tableau montre les changements lors de la transition de l'état 1 à 2 (ou 2-3, 3-4...). Le changement d'état est affiché dans les diagrammes d'état p-V et T-S. Vous pouvez activer/désactiver l'affichage dans le tableau et le graphique avec le bouton correspondant. La colonne intitulée "Somme" contient la somme des changements.
Si n="?", les valeurs (m,p,V,T) sont identiques aux points correspondants 1-2, 2-3,...
Pour les valeurs sélectionnées de n :
• n=0, p=const, Isobare, (dp=0,wt=0,q=Δh,w=Δh−Δu)
• n=1, T=const, Isotherme, (dT=0,Δu=Δh=0,q=w=wt)
• n=κ, s=const, Isentropique, (ds=0,q=0,w=−Δu,wt=−Δh)
• n=∞, v=const, Isochore, (dv=0,w=0,q=Δu,wt=Δu−Δh)
Changement d'entropie
ΔS = S2 - S1 = (cp * Ln(T2/T1) - r * Ln(p2 / p1))*m1
ΔS = S2 - S1 = (cv * Ln(T2/T1) + r * Ln(v2 / v1))*m1
Changement d'énergie interne
ΔU = cv*(T2 - T1) * m1
Changement d'enthalpie
ΔH = cp * (T2 - T1) * m1
Chaleur polytropique.
Transfert d'énergie vers le système sous forme de chaleur (Q>0, lorsque le système reçoit de la chaleur).
Q = m * cn * (T2 - T1)
Q = -((n - kappa) / (kappa - 1)) * W
Travail de volume polytropique. Transfert d'énergie sous diverses formes de travail (W>0, lorsque le système effectue un travail).
W=Q-dU=m * (cn - cv) * (T2 - T1) = m * (r / (n - 1)) * (T1 - T2)
W=m * r * T1 / (n - 1) * (1 - (V1 / V2)^(n-1))
Travail de flux polytropique (technique)
Wt = n * W
W ... Travail de volume polytropique [J]
n .... Exposant polytropique [~]
Deux des diagrammes d'état les plus couramment utilisés sont affichés :
- Pression (p) - Volume (V)
- Température (T) - Entropie (S)
Chaque point est indiqué par un chiffre. Les sections individuelles peuvent être activées/désactivées à l'aide des boutons situés à gauche.
Solution complète du transfert de chaleur à travers une paroi composite (max. 10 couches).
Le calcul comprend :
- Le transfert de chaleur par convection (définition des fluides, du type d'écoulement, définition des objets contournés)
- Le transfert de chaleur par conduction (définition de la paroi, de l'épaisseur et des paramètres des matériaux de chaque couche)
- Le transfert de chaleur par rayonnement (émission de chaleur, irradiation de la paroi)
- la résolution des faisceaux de tubes (échangeurs de chaleur)
- la résolution des surfaces ailetées
Grâce au calcul, vous obtiendrez les paramètres de transfert de chaleur U du milieu (T1) au milieu (T2), la résistance thermique R, les valeurs du flux thermique et bien d'autres.
Le calcul est variable et permet également des calculs partiels, tels que :
- Détermination du coefficient de transfert de chaleur uniquement entre la paroi et Le milieu
- Détermination du coefficient de transfert de chaleur de la paroi seule
- Solutions pour les parois sous vide et les parois en contact direct avec une surface chauffante ou de refroidissement
La définition complète d'une "paroi" peut être enregistrée pour créer une base de données de solutions pouvant être utilisées dans d'autres chapitres du calcul.
Par exemple, le refroidissement/chauffage de tuyauteries et de réservoirs, le calcul d'échangeurs de chaleur et la résolution de problèmes impliquant plusieurs parois différentes.
Procédure pour le calcul complet du transfert de chaleur du milieu 1 au milieu 2 :
- Définissez les conditions aux limites du milieu
- Définissez la forme et les couches individuelles de la paroi
- Sélectionnez la forme et le mode d'écoulement sur la surface de la paroi pour le milieu 1 et 2.
- Définissez les paramètres de transfert de chaleur par rayonnement pour les surfaces interne et externe de la paroi
Le résultat du calcul est le coefficient de transmission thermique global U, la résistance thermique R et les valeurs du flux thermique.
Entrez la température du milieu à l'intérieur et à l'extérieur.
Pour les parois planes, la température à gauche et à droite selon l'image.
Entrez la pression du milieu 1 et 2.
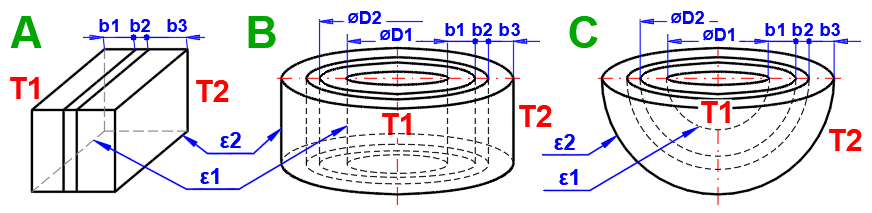
Dans cette section, sélectionnez la forme de la paroi et définissez les paramètres de chaque couche.
Sélectionnez le type de paroi.
Choisissez le groupe de matériaux. Le pointeur dans le tableau des matériaux (ligne suivante) sera réglé sur le premier matériau du type correspondant.
Les courbes de température dans la paroi (surface cylindrique et sphérique) sont remplacées par une droite.
x ... épaisseur de la paroi
y ... profil de température
Sélectionnez le matériau de la couche. En appuyant sur le bouton "Ajouter/Remplacer", le matériau sélectionné est ajouté soit à la ligne dans laquelle la cellule active se trouve, soit à la première ligne sans description dans le tableau de définition ci-dessous. Si la ligne contient déjà des valeurs b, ρ, λ, Cp, elles sont écrasées. Le bouton "Tout effacer" supprime les lignes 2-10.
La liste répertorie les couches individuelles de la paroi.
Une couche est incluse dans le calcul de la paroi si son épaisseur est non nulle.
Si le tableau n'est pas cohérent (par exemple, une ligne vide), l'inscription "Check" est affichée. Vérifiez votre saisie.
Si le type de paroi est cylindrique ou sphérique, il est nécessaire d'entrer le diamètre intérieur de la paroi composite. Les diamètres intérieurs des couches suivantes sont calculés à partir de l'épaisseur de couche saisie.
Épaisseur de la couche de la paroi.
Densité du matériau
Cette valeur n'a aucune influence sur le calcul du transfert de chaleur. Elle est utilisée pour déterminer le poids total de la paroi.
Conductivité thermique
Conversion d'unités
1 [W/m/K] = 0.57782 [BTU/h/ft/F]
1 [BTU/h/ft/F] = 1.7306 [W/m/K]
Capacité thermique massique
Conversion d'unités
1 [J/kg/°K] = 0.0002388459 [BTU/lb/°F]
1 [BTU/lb/°F] = 4186.8 [J/kg/°K]
Résistance thermique de la paroi rapportée à l'unité de surface interne
Conversion d'unités
1 [m²K/W] = 5.6744659 [h.ft²F/Btu]
1 [h.ft²F/Btu] = 0.17622804 [m²K/W]
Thermal resistance of the wall per unit of internal area
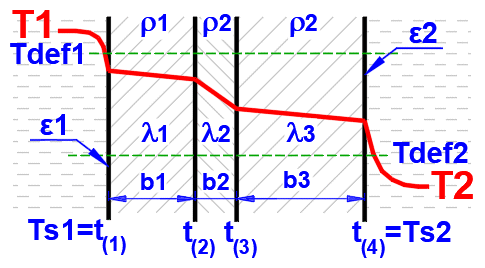
La température sur la première ligne est la température interne (gauche) de la paroi t(1).
Sur les autres lignes, les températures se trouvent à l'interface des couches de la paroi.
Masse de la couche de la paroi rapportée à l'unité de surface interne.
Lors de la sélection d'une surface cylindrique/sphérique, la valeur est recalculée.
Dans cette section, le transfert de chaleur par convection est résolu (le milieu s'écoule sur la surface). L'image montre les options. Pour la résolution, il est nécessaire de définir les paramètres du milieu, le type d'écoulement et les paramètres de la surface sur laquelle le fluide s'écoule.
A) Convection forcée à l'intérieur d'un profil (01-06)
B) Convection forcée autour d'un profil (07-13)
C) Convection naturelle - écoulement provoqué par la différence de densité du milieu chauffé/refroidi (14-19)
En outre, il est possible de résoudre l'écoulement autour d'un faisceau de tubes et l'écoulement sur un profil aileté.
Le calcul peut être utilisé de deux manières.
A) Transfert de chaleur complet de Medium 1 à Medium 2
Dans ce cas, la chaîne de calcul doit être maintenue (T1=>Ts1=>Ts2=>T2). Les cases à cocher sous [4.14] doivent être cochées.
B) Résolution du transfert de chaleur entre la paroi et le milieu
Il est possible, après avoir décoché la case [4.14], d'entrer directement la température de la paroi. Dans ce cas, seul le transfert de chaleur par convection pour la paroi donnée est résolu. Le résultat valide est alors uniquement la valeur du coefficient de transfert de chaleur hc, ou hc+hr pour le côté sélectionné de la paroi.
La liste contient les problèmes les plus fréquemment résolus. En sélectionnant dans la liste, le type d'écoulement 1 et 2 correspondant est défini et les interrupteurs pour l'utilisation des valeurs suggérées (champ vert) sont activés.
Ici, définissez les paramètres du milieu à l'intérieur et à l'extérieur (gauche et droite).
Les options suivantes sont disponibles :
A - Vide. Si un vide se trouve sur le côté de la paroi, le transfert de chaleur par convection est nul.
B - Connexion directe. Une source de chaleur/froid est directement connectée au côté de la paroi, et le transfert de chaleur a lieu avec des pertes qui peuvent être négligées. Par exemple, le fond d'une casserole sur un réchaud.
C - Substances liquides et gazeuses numérotées, prédéfinies et fréquemment utilisées. Pour ces substances, les paramètres requis sont définis en fonction de la température (pression).
Si le liquide / le gaz ne figure pas dans la liste, décochez la case dans la ligne avec la valeur de densité et entrez manuellement tous les paramètres du liquide / gaz pour la température de définition Tdef.
Dans le champ vert se trouve la valeur qui est le résultat du calcul complet du transfert de chaleur du milieu 1 au milieu 2 (rayonnement, convection => conduction => convection, rayonnement). Cette valeur est obtenue par une itération progressive de la température de la paroi de manière à ce que les flux thermiques Q1 et Q2 soient identiques.
Après avoir décoché la case, vous pouvez entrer votre propre valeur.
Dans ce cas, le résultat du calcul est le transfert de chaleur par rayonnement + convection sur le côté approprié de la paroi.
Les équations de critère pour le calcul du transfert de chaleur hc par différents auteurs utilisent différentes températures pour définir les paramètres du liquide / gaz.
a) Température moyenne du film à la paroi Tdef = (T + Ts)/2
b) Température moyenne Tdef = T
Dans la plupart des équations, Tdef = (T + Ts)/2 est utilisé.
Si la saisie directe de la valeur (première option) n'est pas choisie, un basculement automatique est effectué lors de la sélection de l'équation de critère [4.23].
Viscosité dynamique pour la température de la paroi Ts
Viscosité dynamique pour la température de définition Tdef
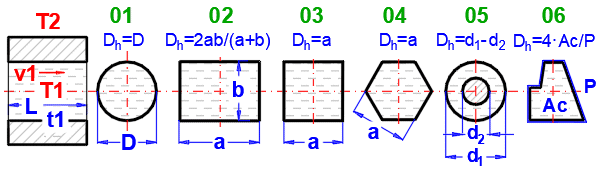
Sélectionnez le type d'écoulement. Dans la liste, la première lettre signifie :
A-Convection forcée
B-Convection naturelle
Le numéro correspond à l'image ci-dessus et la petite lettre après le numéro détermine l'équation (source) qui est utilisée.
Sélectionnez le type d'écoulement pour le milieu 1 et le milieu 2, correspondant à votre problème selon l'image ci-dessus. La combinaison mutuelle de la sélection doit avoir un sens. Par exemple, il n'est pas possible que le milieu 1 s'écoule dans un tube de section circulaire et que le milieu 2 s'écoule autour d'une sphère.
Une combinaison inappropriée est signalée par l'inscription rouge "Check" entre les listes de sélection.
**) Écoulement annulaire 05
Si cette option (05) est sélectionnée comme paroi intérieure (gauche), le transfert de chaleur pour le diamètre extérieur d1 est résolu (entre le liquide en écoulement et l'extérieur).
Si cette option (05) est sélectionnée comme paroi extérieure (droite), le transfert de chaleur pour le diamètre intérieur d2 est résolu (entre le liquide en écoulement et l'intérieur).
La combinaison autorisée est donc :
1) A-05 ... A-07 ou
2) A-01 ... A-05 (approprié si vous souhaitez utiliser des ailettes longitudinales pour la surface extérieure du tube)
Si le type d'écoulement A-Convection forcée est sélectionné, entrez la vitesse d'écoulement.
Après la sélection du type d'écoulement, les noms des variables et les unités sont définis en conséquence, selon l'image.
Les champs verts contiennent les valeurs suggérées.
L'ailetage est une solution efficace pour augmenter la surface de transfert de chaleur et ainsi augmenter le transfert de chaleur.
Si la surface sur laquelle le fluide s'écoule est ailetée, réglez l'interrupteur sur "Oui".
La forme de l'ailette elle-même est définie dans la section 4a. Vous y accédez en appuyant sur le bouton ">>Définition [4a]."
Basé sur les dimensions de l'ailetage (section 4a), une nouvelle surface de transfert de chaleur At1, At2 est déterminée. Elle est utilisée pour les valeurs suggérées A1 et A2 [4.37].
L'ailetage augmente la surface de transfert de chaleur, mais en même temps, il réduit l'efficacité du transfert de chaleur ηf1, ηf2. Le coefficient de transfert de chaleur hc1, hc2 est corrigé par cette efficacité.
Pour augmenter la surface de transfert de chaleur, les faisceaux de tubes sont souvent utilisés. Si vous souhaitez résoudre ce problème, choisissez la disposition des tubes A ou B dans la liste (voir image). Dans les lignes suivantes, remplissez les paramètres de la disposition des tubes. Pour ce problème, il est nécessaire que le milieu 1 s'écoule dans le tube (01-06) et que le milieu 2 s'écoule autour du tube (07-11).
Si une combinaison incorrecte de types d'écoulement est choisie, l'inscription "Check" est affichée.
Entrez la distance entre les tubes dans la direction verticale ST et dans la direction horizontale SL selon l'image.
La valeur par défaut est le double du diamètre extérieur du tube.
Entrez le nombre de rangées dans la direction verticale m et dans la direction horizontale n selon l'image.
En fonction de la disposition et du nombre de rangées et de colonnes, le nombre de tubes dans le faisceau est déterminé (cellule verte).
Si le nombre de tubes dans votre problème est différent, vous pouvez entrer votre propre valeur. Cela affectera la proposition de la surface de transfert de chaleur.
Dans la ligne [4.24], vous entrez la vitesse v2 de l'écoulement avant l'entrée dans le faisceau de tubes. L'insertion des tubes réduit la section d'écoulement. Cela augmente la vitesse d'écoulement autour des tubes (v2max) pour le milieu 2.
Le champ vert contient une valeur suggérée, basée sur les dimensions et la vitesse v2 saisies. Si votre construction est atypique, décochez la case et entrez votre propre valeur.
Dans le champ vert se trouve une valeur suggérée basée sur les paramètres définis précédemment.
Pour le milieu 1, c'est le côté gauche (pour une surface) ou le périmètre intérieur x la longueur du tube. Pour le milieu 2, c'est le côté droit (pour une surface) ou le périmètre extérieur x la longueur du tube.
Si l'ailetage ou l'écoulement à travers un faisceau de tubes (échangeurs) est sélectionné, la surface de transfert de chaleur est modifiée en conséquence.
1. Faisceau de tubes ... A * nombre de tubes
2. Ailetage ... At (de la section Ailetage)
3. Faisceau de tubes ailetés ... Cas 1 * Cas 2
Le cas d'un simple écoulement (sans ailetage) est vérifié, où la surface de transfert de chaleur pour le milieu 1 doit être inférieure ou égale à la surface pour le milieu 2. Si ce n'est pas le cas, vous êtes averti par l'inscription "Check".
Lors de l'utilisation d'équations de critère pour le calcul du coefficient de transfert de chaleur hc, des paramètres sans dimension (nombres de similarité) sont utilisés, ce qui permet de résoudre des formes similaires de différentes dimensions et de différentes conditions environnementales. Une explication plus détaillée est fournie dans l'aide ou dans la littérature spécialisée.
Les nombres de similarité les plus importants sont répertoriés ici.
Avec le bouton, vous déplacez la valeur suggérée (calculée) hc1, hc2 de la cellule verte vers la cellule d'entrée. L'itération s'effectue 5 fois.
Le nombre de similarité le plus important est le nombre de Nusselt. Pour le calcul du coefficient de transfert de chaleur hc, les relations suivantes s'appliquent :
Nu = hc Dh / λ ===>
hc = Nu λ / Dh
λ ... Conductivité thermique du matériau de la paroi
Dh ... Dimension caractéristique (D, Dh, a ..... selon la forme)
Dans le champ vert se trouvent les coefficients de transfert de chaleur calculés hc1 et hc2. Le calcul est basé sur les paramètres du milieu en écoulement, les températures et le type d'écoulement. Si vous souhaitez les utiliser, appuyez sur le bouton "Itération" hc1<<, hc2<<.
Le changement de hc1 et hc2 entraîne naturellement un changement de température, et donc un changement des paramètres du milieu en écoulement et un nouveau calcul de hc. C'est pourquoi le remplacement est effectué 5 fois de suite.
Les petits boutons "hc1" et "hc2" ne remplacent alors qu'un seul coefficient.
Pour chaque milieu, deux valeurs sont indiquées
- flux thermique rapporté à l'unité de surface (A1, A2)
- flux thermique total à travers la surface A1, A2
Dans cette partie du calcul, des cas simples de rayonnement / d'irradiation sont résolus.
- Émission dans l'espace (par exemple, un grand hall)
- Émission dans l'espace (environnement atmosphérique normal)
- Irradiation de la surface (par exemple, rayonnement solaire)
Pour la plupart des situations courantes, ces cas sont suffisants. Si vous avez besoin de résoudre des problèmes plus complexes dans le domaine du transfert de chaleur par rayonnement, utilisez la section [7.0] et utilisez le résultat du calcul comme un flux de rayonnement positif / négatif tombant sur la surface donnée.
L'image indique le flux d'énergie (+) et (-) par rapport à la surface de la paroi 1 et 2.
Choisissez le groupe de matériaux. Le pointeur dans le tableau des matériaux (ligne suivante) sera réglé sur le premier matériau du type correspondant.
Le bouton "Search" tentera de trouver le matériau correspondant à la première et à la dernière couche de la paroi dans le tableau des matériaux.
Sélectionnez le matériau de la surface. L'émissivité typique pour le matériau sélectionné est indiquée entre parenthèses après le nom. Si un intervalle de valeurs est indiqué, leur moyenne est proposée comme valeur suggérée (verte).
Après avoir décoché la case, vous pouvez entrer votre propre valeur d'émissivité pour la surface de la paroi.
Déterminez si la chaleur est émise dans l'espace.
Choisissez l'option correspondante (voir image)
A ... Pas de transfert de chaleur par rayonnement. Il s'agit d'une surface fermée (par exemple, la paroi intérieure d'une tuyauterie).
B ... Émission générale dans l'espace (intérieur et extérieur). Pour le calcul du transfert de chaleur par rayonnement, la température du milieu T1 ou T2 est utilisée par rapport à la température de la paroi Ts1 ou Ts2.
Si vous ne connaissez pas les conditions exactes, choisissez cette option.
C, D, E ... Pour déterminer le rayonnement entre la paroi et le ciel, la température équivalente du ciel pour un corps noir Tsky [°K] est définie. Cette température tient compte de l'inégalité de la température de l'atmosphère et du rayonnement dans certaines longueurs d'onde.
Calcul du flux thermique qr' = ε σ (Tsky^4 - Ts^4)
Pour la relation entre la température du ciel et la température de l'air local, des relations approximatives sont utilisées :
C ... Tsky = Ta - 6°C
D ... Tsky = Ta - 12°C
E ... Tsky = 0.0552 Ta^1.5 (validité -30...+50°C)
où Ta ... température de l'air ambiant [°K] (par exemple : Ta = T2[°C] + 273.15)
Dans le champ vert se trouve la valeur suggérée de la surface d'émission. Si l'ailetage ou le faisceau de tubes n'est pas utilisé, la surface Ar1, Ar2 est identique à la surface de transfert de chaleur A1 ou A2 [4.37].
Si l'ailetage ou l'écoulement à travers un faisceau de tubes est choisi, la surface d'émission est modifiée en conséquence.
1. Faisceau de tubes ... A * nombre de tubes extérieurs / 2
2. Ailetage ... A + surface des ailettes extérieures
3. Faisceau de tubes ailetés ... cas 1 * cas 2
Pour chaque milieu, deux valeurs sont indiquées
- flux thermique rapporté à l'unité de surface (A1, A2)
- flux thermique total à travers la surface A1, A2
Si vous avez besoin de résoudre un autre transfert de chaleur par rayonnement que l'émission dans l'espace. Par ex. : rayonnement solaire, données de la section [7.0], votre propre calcul...
Entrez l'intensité du rayonnement tombant sur la surface. Avec le sélecteur à droite, vous réglez :
- * 1 : Le calcul utilise directement la valeur saisie et ne prend pas en compte l'émissivité de la paroi ε. Il est supposé que l'émissivité est déjà incluse dans la grandeur du rayonnement. Par exemple, le résultat du calcul de la section [7.0].
- * ε : Le calcul multiplie la valeur saisie par le coefficient d'émissivité ε de la paroi sélectionné ci-dessus. Il est supposé que le niveau de rayonnement est connu. Par exemple, le rayonnement solaire.
Rayonnement solaire
Sa valeur maximale à la surface de la Terre est d'environ 1100 [W/m²] (350 [Btu/h/ft²]). Pour des valeurs précises, utilisez la section [8.0].
Entrez / Choisissez la taille de la surface irradiée Ai.
Après avoir sélectionné le premier élément de la liste, vous pouvez entrer directement la taille de la surface irradiée Ai.
Les autres éléments 1-5 (voir image) permettent de calculer la surface irradiée Ai à partir de la surface de transfert de chaleur A1, A2 en fonction de sa forme.
Pour chaque côté de la paroi, deux valeurs sont indiquées
- flux thermique moyen rapporté à l'unité de surface A1, A2 (puisque seule une partie de la surface de transfert de chaleur peut être irradiée, la valeur d'entrée "ir" est multipliée par le rapport Ai/A).
- flux thermique total à travers la surface
Somme de toutes les composantes.
Coefficient de transfert de chaleur pour le côté approprié de la paroi. Il comprend la convection, l'émission et l'irradiation.
Flux thermique pour le côté approprié de la paroi. Il comprend la convection, l'émission et l'irradiation.
Le calcul ne résout pas un éventuel changement de température du milieu en écoulement.
qcri' = qc' + qr' + qi' ... spécifique rapporté à l'unité de surface intérieure / extérieure
Qcri = Qc + Qr + Qi ... total
Pour chaque milieu, deux valeurs sont indiquées
- flux thermique rapporté à l'unité de surface
- flux thermique total à travers la surface A1, A2
Pour d'autres calculs, il est nécessaire de connaître le coefficient global de transmission thermique U ou la résistance thermique R=1/U. Dans les calculs, on utilise :
1) Des valeurs rapportées à la surface interne (1) ou externe (2). Elles sont également valables pour le cylindre et la sphère.
2) Des valeurs rapportées à la longueur unitaire du cylindre défini [4.5, 4.8].
3) Des valeurs rapportées à la sphère définie [4.5, 4.8].
Dans la littérature, les catalogues mentionnent souvent le paramètre "Résistance thermique de la paroi". Il s'agit uniquement de la résistance thermique de la paroi composite définie dans le tableau ci-dessus.
Pour une orientation rapide, le calcul du chauffage / refroidissement du milieu de travail est également inclus, si le problème résolu le permet (calcul complet, longue tuyauterie, longues surfaces sur lesquelles le fluide s'écoule, etc.).
Avec le sélecteur entre les titres, vous choisissez si les milieux s'écoulent à co-courant ou à contre-courant.
Ci-dessous, entrez les paramètres du milieu en écoulement pour le côté intérieur (gauche) et pour le côté extérieur (droit) de la paroi pour les températures T1 et T2.
Lors du calcul de la section d'écoulement suggérée (cellule verte), les cas suivants peuvent se produire :
1) Le fluide s'écoule à travers une section précisément définie (01-06). La valeur dans le champ vert est précise. Par ex. un tube de section circulaire Af = PI * (D/2)^2
2) Le fluide s'écoule autour d'une tuyauterie (07-11). Une valeur est suggérée, qui est égale à la section transversale perpendiculaire de la tuyauterie (dimension extérieure). Par ex. un tube circulaire Af = D * L
3) Le fluide s'écoule à travers un faisceau de tubes. Af = m * ST * L
4) Convection naturelle (13-19). La section d'écoulement est égale à la surface sur laquelle le fluide s'écoule.
Après avoir décoché la case, vous pouvez entrer votre propre valeur.
À partir de la vitesse d'écoulement saisie v1 (v2) [4.24], de la section d'écoulement Af et de la densité Rho, le débit est calculé.
Dans la liste à droite, vous pouvez sélectionner les unités à afficher.
À partir de la surface de transfert de chaleur saisie A [4.37], de la section d'écoulement Af, de la densité Rho, de la capacité thermique massique Cp', du débit m' et du coefficient de transfert de chaleur calculé U, la température de sortie Tout1 et Tout2 est calculée.
Le flux thermique est calculé à partir de la différence de température du milieu à l'entrée et à la sortie et des propriétés du milieu de travail.
Le flux thermique diffère donc des données Qcri [4.62], où le changement de température du milieu n'est pas pris en compte.
Pour chaque milieu, deux valeurs sont indiquées
- flux thermique moyen rapporté à l'unité de surface
- flux thermique total à travers la surface A1, A2
La résolution du transfert de chaleur de la paroi nécessite la saisie et la sélection de dizaines de paramètres. Il est donc possible de nommer et de commenter la solution et de l'enregistrer dans une liste pour une utilisation future, ou pour charger des paramètres dans d'autres sections de ce calcul.
Pour enregistrer l'état actuel de tous les paramètres - la solution - utilisez le bouton "Enregistrer la solution".
Les solutions sont enregistrées sur la feuille de calcul "Parois". Une ligne contient une solution enregistrée.
Lorsque vous appuyez sur le bouton "Enregistrer la solution", la liste est parcourue et si un enregistrement avec le même nom existe, il est écrasé par l'état actuel. S'il n'existe pas de nom dans la liste des solutions, la dernière ligne remplie sur la feuille de calcul "Parois" est trouvée et la solution actuelle est écrite sur la ligne suivante.
La feuille de calcul "Parois" est librement accessible et peut être éditée normalement avec les outils d'Excel (par exemple, la suppression des solutions inutiles - lignes).
Obtention d'une seule valeur à partir d'une solution enregistrée.
Si vous avez besoin d'obtenir une valeur spécifique et de l'utiliser dans votre propre formule, la fonction GetWallProp est préparée pour le faire.
Syntaxe :
GetWallProp(ID;value_name)
ID ... Numéro de la ligne sur la feuille de calcul "Parois" qui contient la solution enregistrée
value_name ... Nom de la valeur que vous souhaitez obtenir.
Entrez le nom de la solution de transfert de chaleur de la paroi.
Sous ce nom, la solution sera enregistrée dans la liste des solutions enregistrées.
Texte généré automatiquement, qui est ajouté à la description et contient des informations de base, notamment :
T1(),T2() ... Températures, (milieu)
|mm| ... Épaisseur de la paroi
U1 ... Coefficient de transfert de chaleur
q1,q2 ... Flux thermique spécifique total
Entrez une description. Cela vous permettra de mieux vous orienter lors de la consultation ultérieure des solutions déjà enregistrées.
Après avoir sélectionné une solution dans la liste de sélection ci-dessous, appuyez sur le bouton "Charger la solution".
Les boutons à droite vous permettent de vous déplacer dans la liste des solutions enregistrées.
La date d'enregistrement de la solution est au format "aaaammjj - hh:mm:ss".
La liste de sélection contient les solutions de transfert de chaleur de la paroi qui sont enregistrées sur la feuille de calcul "Parois".
Informations de base sur la solution de transfert de chaleur de la paroi sélectionnée.
Description de la solution de transfert de chaleur de la paroi sélectionnée.
Cette section est directement liée à la section précédente et traite de l'ailette de la surface soumise à l'écoulement. Elle est utilisée pour augmenter la surface d'échange thermique et ainsi améliorer le transfert de chaleur. Pour l'utiliser, l'ailette doit être activée dans la section précédente [4.29].
En fonction du type d'écoulement choisi dans la section précédente [4.23], le type d'ailette correspondant, 1-4, est assigné selon la figure.
Les valeurs λ, hc, T et Ts de la section précédente [4.0] sont utilisées pour le calcul de l'ailette. Pour la conductivité thermique du matériau λ, la valeur de la première et de la dernière couche de la paroi composite est utilisée.
En fonction du type d'écoulement choisi [4.23] et des dimensions saisies, la largeur du champ d'ailettes "a" est calculée pour les types d'ailettes suivants :
1) a = longueur de la surface
2) a = longueur du tube
3) a = circonférence interne du tube
4) a = circonférence externe du tube
Vous pouvez saisir votre propre valeur de largeur de champ après avoir décoché la case.
Sélectionnez la forme de l'ailette selon la figure.
En fonction des dimensions de la surface à ailettes et du type d'écoulement, les dimensions de l'ailette sont prédéfinies (cellules vertes). Vous pouvez saisir vos propres dimensions après avoir décoché la case.
La cellule verte propose le nombre maximal d'ailettes pouvant être utilisées en fonction de la largeur du champ et des dimensions de l'ailette. Vous pouvez saisir votre propre valeur après avoir décoché la case. Par exemple, si seule une partie de la surface / du tube est munie d'ailettes.
- Af ... Surface d'une seule ailette (uniquement l'ailette).
- At ... Surface d'échange thermique totale (surface de l'ailette x nombre d'ailettes + surface restante du profil de base).
La valeur de la surface d'échange thermique totale à ailettes At est utilisée comme valeur recommandée à la ligne [4.37].
Le paramètre x sert à trouver l'efficacité de l'ailette dans les graphiques correspondants (il effectue le calcul).
L'efficacité globale inclut le rapport de la surface des ailettes à la surface totale à ailettes et est utilisée lors du calcul du flux thermique qc', Qc [4.43].
Cette section traite de la variation de la température d'un fluide s'écoulant dans une tuyauterie et du temps de refroidissement pour une chute de température donnée dans les tuyauteries, les récipients et les réservoirs.
Sélectionnez le fluide s'écoulant dans la tuyauterie.
Si le fluide n'est pas dans la liste, entrez la valeur de Cp à la ligne [5.3].
Entrez la température de définition. La valeur de Cp pour le fluide sélectionné sera calculée à partir de cette température à la ligne [5.3].
La valeur par défaut (champ vert) est la température T1 de la section [4.0].
Après avoir décoché la case, vous pouvez entrer votre propre valeur de Cp.
Le calcul permet de déterminer la température du fluide s'écoulant dans la tuyauterie à une distance donnée de l'entrée.
Il est supposé que la température ambiante est constante.
La température de changement de phase du fluide n'est pas contrôlée.
Les champs verts contiennent les valeurs de conception tirées de la section [4.0].
Après avoir décoché la case, vous pouvez entrer vos propres valeurs.
Il est nécessaire d'entrer le coefficient de transfert de chaleur rapporté à l'unité de longueur de la tuyauterie.
La valeur Pw indique la puissance perdue (-) ou la puissance gagnée (+).
Le calcul permet de déterminer le temps de refroidissement d'un fluide dans un réservoir (récipient, tuyauterie) de la température T1s à la température T1e.
Il est supposé que la température ambiante est constante.
La température de changement de phase du fluide n'est pas contrôlée.
Les champs verts contiennent les valeurs de conception tirées de la section [4.0].
Après avoir décoché la case, vous pouvez entrer vos propres valeurs.
Entrez la température finale que vous souhaitez atteindre. Le résultat du calcul sera le temps nécessaire pour atteindre la température T1e.
Entrez la masse du fluide dans le réservoir (récipient, tuyauterie).
Entrez le coefficient de transfert de chaleur rapporté à l'unité de surface interne du réservoir.
La valeur E indique la perte d'énergie (-) ou le gain d'énergie (+).
Cette section traite des types de base d'échangeurs de chaleur (co-courant, contre-courant, co-courant+contre-courant, co-courant+contre-courant composé, courant croisé).
Sélectionnez le type d'échangeur de chaleur que vous souhaitez étudier. Référez-vous aux figures A-G pour votre sélection.
Les calculs traitent des problèmes de base. Néanmoins, il est également possible de l'utiliser pour la résolution de types d'échangeurs de chaleur plus complexes si vous connaissez leur facteur de correction [6.17].
Le calcul de l'échangeur de chaleur dépend de la détermination correcte du coefficient global de transfert de chaleur U. Vous le déterminez précisément dans la section [4.0]. Vous pouvez charger les valeurs actuelles de la section [4.0] ou sélectionner une solution de paroi enregistrée dans la liste et charger ses valeurs.
Si vous connaissez le coefficient global de transfert de chaleur, vous pouvez le saisir directement sur la ligne [6.21]. L'aide contient également des valeurs caractéristiques pour les configurations courantes.
En appuyant sur le bouton à droite, les éléments suivants sont chargés :
- Le coefficient global de transfert de chaleur
- Le choix du fluide de travail
- les températures T1, T2
- Le débit massique
Sélectionnez les fluides de travail utilisés dans l'échangeur. Si un fluide ne figure pas dans la liste, saisissez les valeurs de Cp1 et Cp2 sur la ligne [6.7].
Saisissez la température de définition. La valeur de Cp pour le fluide sélectionné sera calculée à partir de cette température sur la ligne [6.7]. La valeur par défaut (case verte) est la moyenne des températures T1in et T1out (ou T2in et T2out pour T2def).
En décochant la case, vous pouvez saisir votre propre valeur de Cp.
Calcul du flux thermique Q pour les paramètres de débit massique et les températures des fluides de travail saisis.
Les lignes suivantes indiquent les paramètres des fluides de travail 1 et 2 (débit massique, température d'entrée, température de sortie). La case verte contient la valeur de conception nécessaire pour atteindre l'équilibre du flux thermique (validité de Q1 = - Q2).
À côté de la case verte se trouve un bouton "◄" qui transfère la valeur de conception vers la valeur d'entrée.
À chaque modification d'une valeur d'entrée, les valeurs correspondantes pour atteindre l'équilibre du flux thermique (Q1 = - Q2) sont recalculées dans les cellules vertes.
Par exemple, une solution absurde du type :
- le fluide de travail 1 avec une température de T1
Le flux thermique entre les fluides 1 et 2. Le flux thermique doit être identique en magnitude (+/-). En fonction du flux thermique, il est ensuite possible de déterminer la taille de la surface d'échange de chaleur.
Après avoir défini le débit massique, les températures et donc le flux thermique, la différence de température moyenne logarithmique ΔT' est établie. Celle-ci est nécessaire pour calculer la surface d'échange de chaleur requise.
Les coefficients R et P sont nécessaires pour déterminer ɛ [6.17].
R ... Le rapport de capacité thermique R
R = (T1Kin - T1Kout) / (T2Kout - T2Kin)
P ... L'efficacité thermique P
P = (T2Kout - T2Kin) / (T1Kin - T2Kin)
Les graphiques correspondants pour ɛ pour de nombreux types d'échangeurs sont disponibles dans la littérature citée.
Pour les types d'échangeurs plus complexes, un facteur de correction ɛ est utilisé pour déterminer la différence de température moyenne logarithmique. Pour les échangeurs de type C-G, il est déterminé par approximation à partir des tableaux (qui se trouvent sur la feuille "Tableaux").
Pour les échangeurs qui ne sont pas définis dans ce programme, le coefficient ɛ peut être déterminé à partir des graphiques R-P-ɛ que l'on peut trouver dans la littérature spécialisée (par exemple, *Heat Exchanger Design Handbook* et autres). Les graphiques sont généralement fournis pour de nombreux types d'échangeurs.
La valeur du coefficient est comprise entre 0.5 et 1.0.
L'échangeur peut être calculé comme un échangeur à plaques ou un échangeur tubulaire. La construction de l'échangeur détermine généralement quelle méthode est la plus avantageuse. Sélectionnez le type dans la liste.
- Échangeur à plaques
Le coefficient global de transfert de chaleur U est défini par unité de surface.
La surface d'échange de chaleur est calculée pour le flux thermique requis.
- Échangeur tubulaire
Le coefficient global de transfert de chaleur U est défini par unité de longueur de tube.
La longueur du tube est calculée pour le flux thermique requis.
Si vous chargez la définition de la paroi à partir de la section [4.0] ou de la liste, la valeur correspondante se trouve dans la case verte. Si vous souhaitez saisir votre propre valeur, décochez la case.
Plage indicative des valeurs de Upl pour différentes combinaisons de fluides dans les échangeurs de chaleur.
Selon le type choisi [6.19], la surface ou la longueur du tube requise est calculée.
Par le calcul, vous déterminez les températures de sortie T1Out et T2Out en fonction de la taille de la surface d'échange de chaleur ou de la longueur du tube.
Saisissez la taille de la surface d'échange de chaleur, ou la longueur du tube.
Pour les paramètres saisis :
- m1', m2' ... [6.9]
- T1in, T2in ... [6.10]
- Upl ou Ucyl ... [6.21]
- A ou L ... [6.24]
vous déterminez les températures de sortie T1Out et T2Out.
En appuyant sur le bouton "▲T1out, ▲T2out", les valeurs calculées sont transférées à la ligne [6.11].
Une simple conversion de la surface en longueur de tube et vice versa. En fonction du type d'échangeur choisi [6.19], la surface [6.22] est convertie en longueur de tube ou la longueur du tube [6.22] en surface.
- Sélectionnez le profil de tube dans la liste (A-E)
- Saisissez la surface ou la longueur du tube (valeur par défaut de [6.22])
- Saisissez les dimensions du profil selon le schéma (les valeurs par défaut sont celles de la paroi chargée [6.3, 6.4])
Pendant le fonctionnement, la surface peut se recouvrir de dépôts ou d'oxydation. Cela augmente la résistance et réduit les performances de l'échangeur. L'augmentation de la résistance est exprimée par le coefficient d'encrassement Rf = 1/Ud - 1/Uc [m²K/W], [h·ft²F/Btu].
Le coefficient est déterminé expérimentalement ou il est possible d'utiliser le tableau des valeurs recommandées [6.35] pour différents fluides.
Saisissez le coefficient global de transfert de chaleur pour une surface propre.
Saisissez le coefficient d'encrassement Rf. Si vous ne connaissez pas la valeur (par exemple, à partir d'une mesure), vous pouvez vous fier aux valeurs du tableau. Si les deux surfaces de l'échangeur sont encrassées (interne et externe), saisissez la somme des Rf.
Le coefficient de transfert de chaleur pour la surface encrassée et la différence de pourcentage entre Uc et Ud. Diminuez la valeur Upl (Ucyl) [6.21] de la différence de pourcentage correspondante.
Le bouton "▲U" diminuera directement la valeur Upl (Ucyl) [6.21].
La température moyenne (Tin+Tout)/2 est affichée en pointillé.
Bleu ... fluide 1
Vert ... fluide 2
Échanger
En appuyant sur le bouton "<---->" vous échangez le fluide 1 et le fluide 2 et vice versa.
Cette section traite des problèmes de base du transfert de chaleur par rayonnement.
A…Rayonnement vers l'espace (surface plane, cylindre, sphère, forme générale)
Pour le rayonnement vers l'espace libre dans l'atmosphère terrestre, la relation Tsky = Température de l'air - 6°C ou Tsky = Température de l'air - 12°C est souvent utilisée (estimation incluant l'effet du rayonnement atmosphérique). Pour l'espace cosmique, il est possible d'utiliser Tsky = -270°C.
B…Rayonnement entre deux surfaces parallèles (surface plane, cylindre, sphère)
C…Rayonnement entre deux surfaces parallèles avec une feuille de blindage x (surface plane, cylindre, sphère)
D…Rayonnement entre deux surfaces parallèles avec deux feuilles de blindage x,y (surface plane, cylindre, sphère)
Hypothèses et simplifications :
1) Le milieu entre les surfaces doit être diatherme. Le type de milieu (vide, type de gaz...) n'est pas traité.
2) Pour le calcul, on considère une feuille d'épaisseur "nulle" et de conductivité thermique "infinie".
3) Dans le cas d'une surface plane, la distance entre les surfaces doit être plus petite d'un ordre de grandeur que les dimensions des surfaces.
4) Dans le cas d'une surface cylindrique, on suppose que la longueur du cylindre L est d'un ordre de grandeur supérieure au diamètre D.
5) Il est possible de choisir une émissivité différente pour chaque côté de la feuille de blindage.
6) Dans le cas de surfaces non concentriques (4), seules les valeurs du flux de chaleur total Q12 sont valables.
Selon le problème sélectionné, les sections d'entrée — les champs grisés — sont désactivées.
Sélectionnez le groupe de matériaux. L'indicateur dans le tableau des matériaux (ligne suivante) sera réglé sur le premier matériau du type correspondant.
Après avoir décoché le bouton, vous pouvez entrer votre propre valeur dans la plage [0…1].
Entrez la température de la paroi T1, T2.
Dans le cas où le rayonnement vers l'espace est traité, entrez la température de l'espace Tsky.
Sélectionnez le type de surface dans la liste.
1. Surface plane : La surface saisie (1) est projetée sur les surfaces 2, X, Y.
2. Surface cylindrique : La longueur du cylindre de (1) est projetée sur 2, X, Y. Les diamètres du cylindre peuvent être choisis arbitrairement en 1, 2, X, Y à condition que D1.
3. Surface sphérique : Les diamètres peuvent être choisis arbitrairement en 1, 2, X, Y à condition que D1.
4. Surface générale : Elle est destinée au calcul du flux de chaleur entre la surface 1, qui est entièrement enfermée dans la surface 2. La taille de la surface peut être choisie arbitrairement en 1, 2, X, Y à condition que A1. La forme des surfaces mutuelles n'est pas traitée, ce qui peut rendre la température de la feuille de blindage x,y imprécise.
Pour la surface générale, on suppose que les surfaces ne sont pas du tout enfermées l'une dans l'autre.
Basé sur la sélection et les données de la ligne précédente, une valeur calculée de la surface A est proposée. Après avoir décoché le bouton, vous pouvez entrer votre propre valeur.
Condition : A1<=Ax<=Ay<=A2. Un texte rouge signale le non-respect de la condition.
Les paramètres des feuilles de blindage sont similaires à ceux de la paroi, sauf qu'une feuille d'épaisseur "nulle" et de conductivité thermique "infinie" est considérée, et il est nécessaire d'entrer directement l'émissivité des deux côtés.
Entrez l'émissivité de la feuille de blindage pour le côté gauche et le côté droit. Les valeurs de la liste ci-dessus peuvent servir de guide.
Dépend de la sélection [7.07].
Pour le cylindre et la sphère, le diamètre peut être choisi. Les autres valeurs sont définies par la surface 1.
Après avoir décoché le bouton, entrez votre propre valeur.
Condition : A1<=Ax<=Ay<=A2. Un texte rouge signale le non-respect de la condition.
Deux valeurs sont indiquées.
1) Flux de chaleur spécifique par unité de surface. Si la surface A1<>A2 (cylindre, sphère, surface générale), les valeurs sont différentes pour chaque surface.
2) Flux de chaleur total pour la surface saisie.
Cette section aborde la charge thermique de base due au rayonnement solaire (durée, heure, emplacement, orientation de la surface, etc.).
De nombreuses constructions d'ingénierie (et de bâtiment) sont exposées au rayonnement solaire. Le calcul sert à déterminer le flux thermique solaire sur une surface pour des conditions données (orientation de la surface, date, heure, altitude, pollution) et à déterminer l'apport énergétique quotidien total.
Utilisez le bouton "▼▼" pour régler la date et l'heure actuelles.
Entrez le mois et le jour pour lesquels vous souhaitez déterminer la valeur du flux solaire.
Utilisez les boutons -/+ pour modifier les valeurs d'entrée et observer les changements sur les graphiques.
Le nombre entre les boutons - et + indique l'incrément.
Un jour invalide est surligné en rouge.
Entrez l'heure et la latitude pour lesquelles vous souhaitez déterminer la valeur du flux solaire.
Utilisez les boutons -/+ pour modifier les valeurs d'entrée et observer les changements sur les graphiques.
Le nombre entre les boutons - et + indique l'incrément.
Latitudes de villes.
Entrez l'inclinaison de la surface par rapport au plan horizontal (0=horizontal, 90=perpendiculaire).
Entrez l'azimut de la normale de la surface (0=S, 90=W, -90=E, 180=N).
Exemple : orientation SW=45.
Utilisez les boutons -/+ pour modifier les valeurs d'entrée et observer les changements sur les graphiques.
Le nombre entre les boutons - et + indique l'incrément.
Les heures de lever et de coucher du soleil (pour le centre du soleil) sont données à titre indicatif. Elles ne tiennent pas compte de la longitude, de l'heure d'été/hiver, etc.
La durée de l'éclairement solaire pour les paramètres d'entrée spécifiés.
Si la combinaison de la date et de la latitude mène à :
Jour polaire … lever/coucher du soleil = 0/24, durée d'éclairement = 24
Nuit polaire … lever/coucher du soleil = 12/12, durée d'éclairement = 0
L'angle d'élévation du soleil φ est l'angle entre le soleil et l'horizon (idéal) pour les paramètres spécifiés MM,JJ,HH.
La déclinaison solaire δ est l'angle du soleil par rapport au plan de l'équateur pour la date spécifiée MM,JJ.
(φ=0) ... Lever et coucher du soleil : Le moment où le centre géométrique du soleil traverse l'horizon.
(φ=-6) ... Le crépuscule civil commence ou se termine au moment où le centre du disque solaire se trouve à 6° sous l'horizon. Pendant le crépuscule civil, il est possible d'effectuer des activités courantes à l'extérieur sans éclairage artificiel, comme lire un journal ou jouer à des jeux de balle.
(φ=-6...-12) ... Crépuscule nautique : Pendant le crépuscule nautique, le centre du disque solaire se trouve entre 6° et 12° sous l'horizon. Les premières étoiles sont visibles et l'horizon est clairement reconnaissable.
(φ=-18) ... Crépuscule astronomique : Le crépuscule astronomique apporte les premiers et derniers rayons de soleil de la journée. Le ciel est très sombre, les étoiles sont très visibles. Si le soleil descend à plus de 18° sous l'horizon, la nuit astronomique commence. Si le soleil, autour du solstice d'été, ne descend pas plus de 18° sous l'horizon, le crépuscule astronomique du soir se confond avec l'aube du matin et la nuit astronomique n'a pas lieu.
Le flux de rayonnement solaire en dehors de l'atmosphère varie de +/-3.3% au cours de l'année (distance Terre-Soleil). La valeur à la distance moyenne Terre-Soleil est de 1367 W/m².
D'autres réglages précisent le flux de rayonnement en fonction de l'atmosphère, de la pollution, etc.
L'altitude définit l'épaisseur et la densité de la couche d'air, ce qui influence la densité du flux thermique.
La sélection dans la liste déroulante transfère la valeur dans la cellule d'entrée.
Il inclut les effets de la pollution atmosphérique pour différentes régions et saisons.
Z=1 ... Passage dans un air complètement propre
Z=2 ... Régions montagneuses
Z=3 ... Campagne
Z=4 ... Ville
Z=>5 ... Zone industrielle
Pour la période d'hiver - 20%
Pour la période d'été + 10%
La sélection dans la liste déroulante transfère la valeur dans la cellule d'entrée.
γs ... L'azimut du soleil est l'angle entre le sud (S) et la position du soleil pour les valeurs d'entrée spécifiées.
Θ ... L'angle d'incidence du rayonnement solaire est l'angle entre la ligne reliant le centre du soleil et la normale "n" de la surface pour les valeurs d'entrée spécifiées.
QbT ... La valeur réelle du rayonnement qui frappe la surface inclinée définie (inclinaison et orientation).
Qbn ... Le rayonnement qui frappe une surface perpendiculaire (à la position du soleil) après avoir traversé l'atmosphère pour les données d'entrée spécifiées (date, lieu, pollution...).
QdT ... Le rayonnement solaire diffus sur la surface donnée.
Qdt = ((1 + cos(beta)) / 2) * Qd
Qd ... Une estimation simplifiée est utilisée, qui considère qu'environ un tiers du rayonnement solaire "perdu" dans l'atmosphère frappe la surface horizontale.
Qd = 0.33 * (Qon - Qbn)
Albédo - Le rapport entre la densité de flux de rayonnement solaire réfléchie et celle qui a frappé la surface. Pour les calculs, on peut utiliser Rhog = 0.2
Valeurs :
0.10 à 0.15 ... Végétation courante
0.90 ... Neige
0.35 - 0.45 ... Surface terrestre : terre ferme
0.05 - 0.10 ... Surface terrestre : mer
0.30 (moyenne) ... Albédo de la Terre (planète)
QrT ... Rayonnement solaire réfléchi sur une surface donnée.
Qrt = Rhog * ((1 - cos(beta)) / 2) * (Qb + Qg)
Entrez la taille de la surface irradiée.
L'irradiance solaire sur une surface orientée de manière générale pour l'heure et la position spécifiées. La somme de toutes les composantes (directe, diffuse, réfléchie).
QT ... Énergie totale sur la surface spécifiée
QT' ... Énergie par unité de surface
Cette valeur indique la quantité de rayonnement solaire convertie en énergie utilisable. En général, les valeurs suivantes peuvent être choisies. Les valeurs exactes sont disponibles auprès du fabricant ou du fournisseur.
Conversion directe en électricité :
Panneaux photovoltaïques - L'efficacité des panneaux modernes (année 2025) se situe dans une fourchette de 18-24% (pour 25C). Elle dépend de la température, jusqu'à -20% en été, et jusqu'à +10% en hiver.
Chauffage de l'eau, chauffage des locaux :
L'efficacité dépend de la température du fluide chauffé, de la conception, etc. Les valeurs indicatives suivantes peuvent être utilisées. La température du fluide de travail est entre parenthèses.
Capteurs plans - 95% (0C), 70% (40C), 40% (80C), 20% (100C)
Capteurs à tubes sous vide : 70% (0C), 55% (40C), 40% (80C), 30% (120C), 20% (140C)
L'irradiance solaire multipliée par l'efficacité.
(spécifique par unité de surface, totale pour la surface)
La puissance de la surface pour le jour spécifié en supposant une couverture nuageuse nulle (spécifique par unité de surface, totale pour la surface).
En fonction de la latitude saisie, l'heure du lever et du coucher du soleil est affichée pour les jours 1 à 365.
Déclinaison ... L'angle du soleil par rapport au plan de l'équateur (δ) pour le jour (1-365).
Affichage de l'évolution des valeurs pour les jours 1 à 365 :
- Constante solaire (Qon) [W/m²].
- Hauteur du soleil au-dessus de l'horizon (φ) pour l'heure spécifiée.
- Puissance de rayonnement (Qbn) [W/m²] sur une surface perpendiculaire au soleil pour l'heure spécifiée.
Affichage de l'évolution des valeurs pour chaque heure (0-24) :
- Hauteur du soleil au-dessus de l'horizon
- Valeur totale du rayonnement solaire (QT=QbT+QdT+QrT)
- Composantes individuelles QbT, QdT, QrT
Les valeurs sont en [W/m²].
Excel contient le complément « Solveur », un outil intégré pour résoudre la programmation linéaire et non linéaire. S'il est nécessaire de résoudre des problèmes de transfert de chaleur plus complexes, vous pouvez préparer ici les données pour ce complément de manière claire et organisée. Cela permet de concevoir un modèle et de résoudre, par exemple, des problèmes où le transfert de chaleur se produit simultanément à travers plusieurs murs différents. Cette section se trouve sur une feuille séparée nommée « Solveur » (la deuxième feuille), et la feuille n'est pas verrouillée.
Procédure :
1. Préparez un tableau des transferts de chaleur résolus pour chaque mur [9.6].
2. Définissez le modèle mathématique à l'aide des relations Excel. [9.5, 9.6, 9.7].
3. Utilisez le complément « Solveur » pour résoudre le modèle.
La section [4.0] traite du transfert de chaleur pour un mur. Vous pouvez transférer les valeurs actuelles ou les valeurs du tableau des solutions enregistrées dans le tableau ci-dessous.
Sélectionnez une solution de mur dans la liste. Lorsque vous cliquez sur le bouton "Ajouter/Remplacer", la solution sélectionnée est ajoutée soit à la ligne où se trouve la cellule active, soit à la première ligne sans description dans le tableau de définition ci-dessous. Si la ligne contient déjà des valeurs, elles sont écrasées. Utilisez le bouton "Tout effacer" pour supprimer toutes les lignes.
Dans la liste de sélection, choisissez la valeur qui sera transférée dans la colonne correspondante. Si vous sélectionnez le premier élément, "Ne pas remplir", la valeur d'origine dans la colonne restera inchangée.
La notation est la même que dans la section [4.0].
Deux colonnes que vous pouvez utiliser pour divers calculs intermédiaires.
Dans le tableau, préparez les valeurs pour tous les murs que vous utiliserez dans le modèle mathématique pour le "Solveur".
L'utilisation du complément "Solveur" nécessite la définition d'un modèle mathématique qui décrit le problème à résoudre.
Pour plus de simplicité et de clarté, trois zones ont été préparées (valeurs d'entrée, valeurs de sortie et contraintes). Ici, vous pouvez définir le modèle mathématique correspondant de manière claire à l'aide de formules Excel.
Bien sûr, vous pouvez préparer la mise en page et la définition du modèle mathématique entièrement selon vos propres exigences. Il n'est pas nécessaire de suivre la disposition proposée.
Vous trouverez le lancement du complément "Solveur" dans le menu (ruban) Excel "Données".
Un exemple simple et illustratif d'un problème, de la définition du modèle et du lancement du "Solveur" en trois étapes. L'exemple résout la taille de la source de chaleur QH pour obtenir la température T2 dans une pièce avec quatre murs différents et une température ambiante T2.
Les exemples suivants sont résolus ci-dessous :
Exemple 01 - Tableau périodique des éléments - paramètres de mélange gazeux (m,
r, κ) - air
Exemple 02 - Tableau périodique des éléments - paramètres du gaz (m, r, κ) -
sulfure d'hydrogène
Exemple 03 - Gaz idéal - Remplissage d'une bouteille sous pression
Exemple 04 - Gaz idéal - changement de volume dû à l'apport d'énergie
(changement isobare)
Exemple 05 - Gaz idéal - Mélange de gaz avec différents paramètres (m, p, V, T)
Exemple 06 - Gaz Idéal - Compression Polytropique (Compresseur)
Exemple 07 - Gaz Idéal - Cycle de Compresseur à Piston
Exemple 08 - Transfert de Chaleur Complexe à travers un Tuyau Cylindrique
(Rayonnement, Convection, Conduction)
Exemple 09 - Sauvegarde et Chargement des Solutions de Transfert de Chaleur
Pariétal, Récupération des Valeurs
Exemple 10 - Solution Partielle de Transfert de Chaleur (Rayonnement ou
Convection ou Conduction)
Exemple 11 - Transfert de Chaleur à travers une Paroi avec Vide d'un Côté
(Thermos)
Exemple 12 - Transfert de Chaleur à travers une Paroi Ailetée, Chauffée par
Contact d'un Côté (Générateur Électrique TEG)
Exemple 13 - Transfert de Chaleur - Faisceau de Tubes Circulaires (10 x 8)
Exemple 14 - Transfert de Chaleur - Faisceau de Tubes Cylindriques Ailetés (7 x
6)
Exemple 15 - Changement de Température et Temps de Refroidissement d'un Liquide
dans un Récipient (Thermos)
Exemple 16 - Échangeur de Chaleur - Contre-Courant (Eau / Huile)
Exemple 17 - Échangeur de Chaleur - Simple - Flux Croisé avec Deux Fluides Non
Mélangés
Exemple 18 - Transfert de Chaleur par Rayonnement entre Deux Surfaces Parallèles
Exemple 19 - Transfert de Chaleur par Rayonnement entre Deux Surfaces Parallèles
avec un Film de Protection
Exemple 20 - Rayonnement Solaire - Valeurs pour une Surface Orientée,
Localisation Géographique, Heure et Environnement
Exemple 21 - Bilan Thermique d'un Bâtiment : Solveur, Transfert de Chaleur dans
un Objet, Chauffage, Températures des Pièces
Calcul des paramètres du mélange gazeux - air (Masse molaire ... M, Constante spécifique des gaz ... r, Indice adiabatique ... κ).
Air : un mélange de N2+O2+Ar+CO2
Fraction massique : (N2...75.518, O2...23.1354, Ar...1.288, CO2...0.059)
Entrez le mélange gazeux et utilisez le bouton pour remplir le tableau.
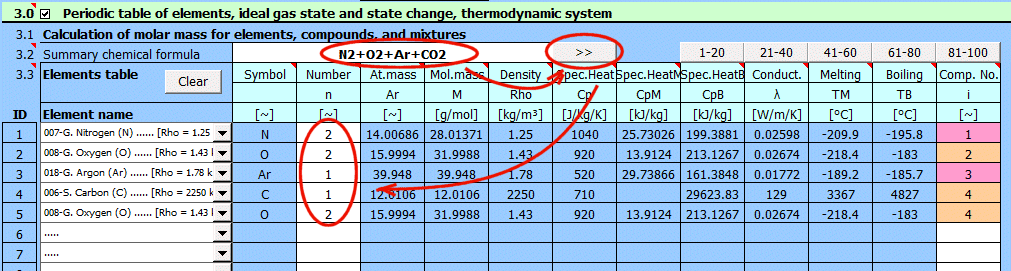
Entrez la fraction massique de chaque composant pour déterminer les valeurs requises du mélange gazeux.

Utilisez le bouton "▼M,κ▼" pour transférer les valeurs vers le calcul des paramètres du gaz idéal.
Calcul des paramètres du gaz - sulfure d'hydrogène (Masse molaire ... M, Constante spécifique des gaz ... r, Indice adiabatique ... κ).
Formule : H2S
Entrez la formule.

La fraction massique est de 100%.
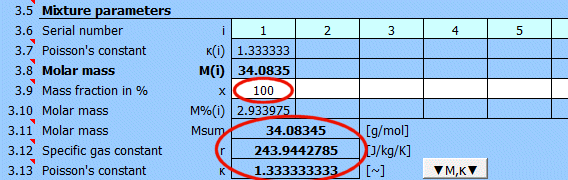
Utilisez le bouton "▼M,κ▼" pour transférer les valeurs vers le calcul des paramètres du gaz idéal.
Comment la masse d'une bouteille sous pression de 15L changera-t-elle si elle est remplie d'air à 20MPa et 20°C ?
Sélectionnez l'air comme substance de travail et réglez la température.

Entrez les propriétés pour une pression atmosphérique de 101kPa.
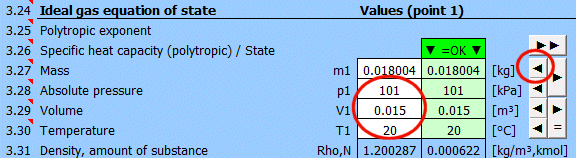
Entrez la nouvelle pression 20MPa = 20000kPa et appuyez sur le bouton.
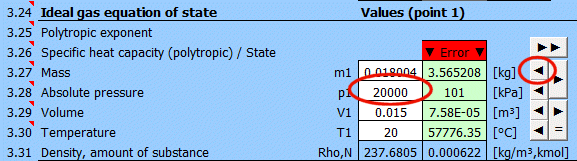
Le résultat est la nouvelle masse du contenu de la bouteille.
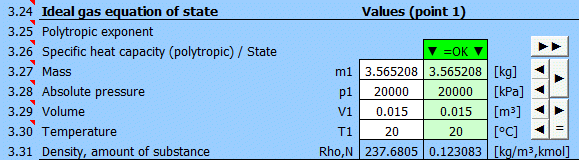
La masse augmentera de 3.565 - 0.0182 = 3.5468kg.
L'air est dans un cylindre sous un piston. 300kJ de chaleur sont ajoutés au cylindre. Déterminez le changement de T et V, p1=p2.
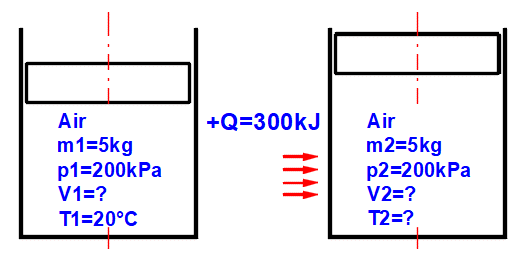
Sélectionnez l'air comme substance de travail et réglez la température.

1. Entrez les valeurs pour m1, p1, T1.
2. Appuyez sur le bouton "◄" pour remplir V1.
3. Utilisez le bouton "►►" pour copier les valeurs aux autres points.
4. Modifiez progressivement la température T2 jusqu'à ce que la valeur Q soit de
300kJ.
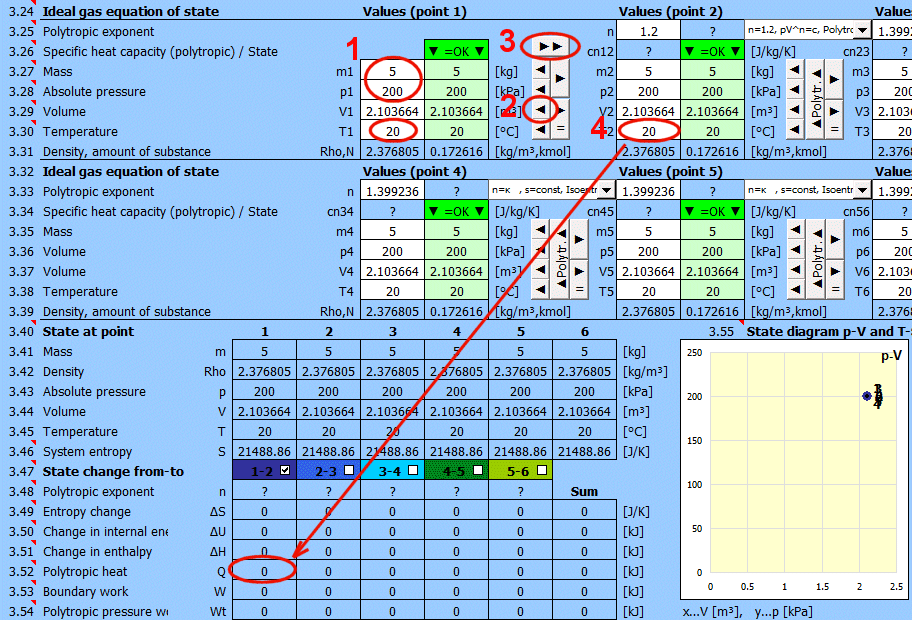
Appuyez sur le bouton "◄" pour remplir V2.
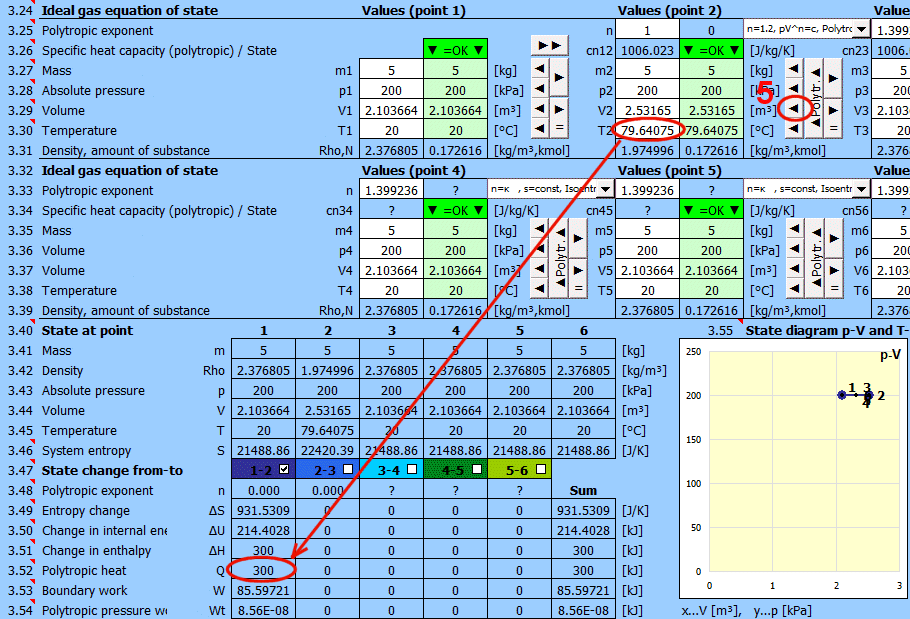
Deux récipients connectés contiennent de l'air avec des paramètres différents. Après l'ouverture de la vanne de connexion, les gaz se mélangeront puis refroidiront jusqu'à une température finale de 25°C.
Déterminez la pression finale, la température, le changement d'énergie...
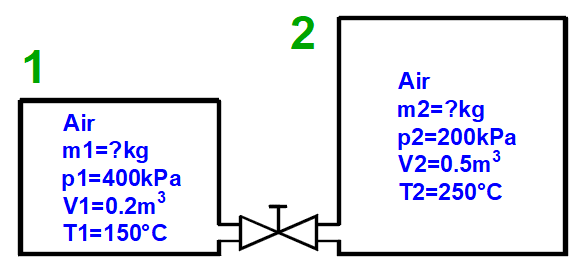
Sélectionnez l'air comme substance de travail et estimez la température à 100°C.

1. Définissez les paramètres pour le récipient 1.
2. Remplissez la masse de gaz correspondante m1.
3. Définissez les paramètres pour le récipient 2.
4. Remplissez la masse de gaz correspondante m2.
5. Appuyez sur le bouton pour calculer les paramètres du mélange résultant.
Le point 3 montre les paramètres de gaz calculés qui se produiront après le mélange 1+2.
6. Transférez les paramètres résultants au point 4.
7. Entrez la température finale de l'ensemble du système T4.
8. Remplissez la pression de gaz correspondante p4.
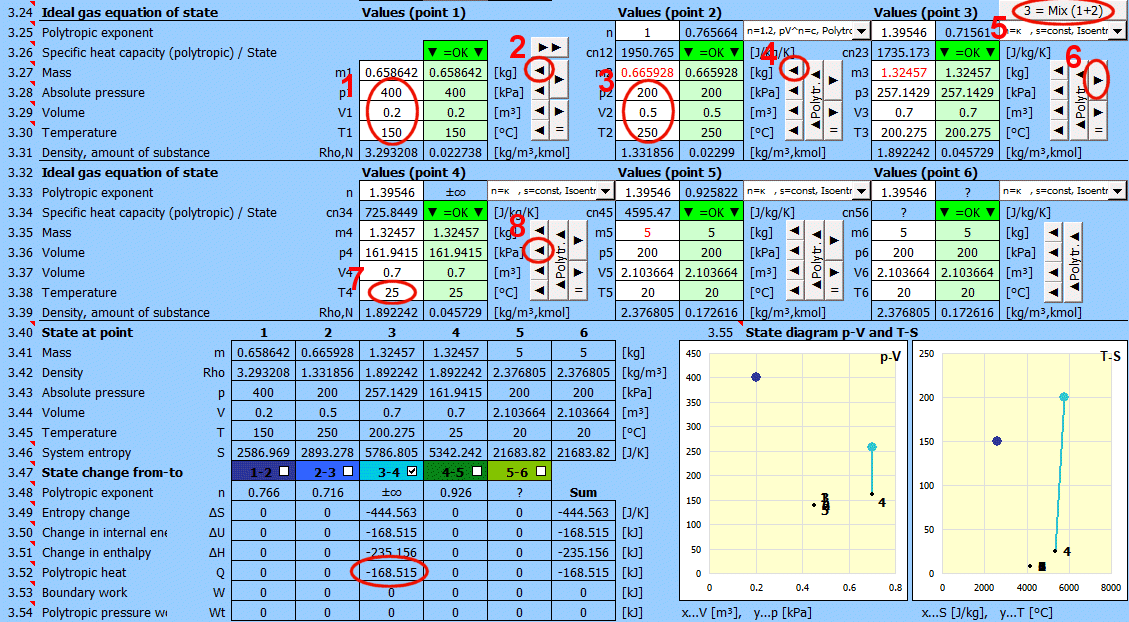
Le changement d'énergie (chaleur retirée Q) est le changement entre 3 et 4. Pour refroidir le mélange (du point 3), 168kJ de chaleur doivent être retirés.
Lors d'un processus polytropique, toutes les variables d'état (p, V, T) changent
généralement. Pour un processus polytropique dans un gaz idéal, l'équation p *
V^n = const s'applique.
Pour un compresseur à piston : n = 1,2–1,3 (Processus avec évacuation partielle
de la chaleur, valeur typique pour les compresseurs lents avec refroidissement).
Paramètres initiaux de l'air : m1=?, p1=150 kPa, V1=260 m^3, T1=27 °C.
Il est comprimé par un compresseur à piston avec un exposant polytropique n=1,2.
Valeurs finales : m2=m1, p2=?, V2=80 m^3, T2=?
Sélectionnez l'air comme fluide de travail et réglez la température.

1. Réglez les paramètres de l'air au point initial 1.
2. Remplissez la masse de gaz correspondante m1 à l'aide du bouton "◄".
3. Utilisez le bouton "►►" pour copier les valeurs aux autres points.
4. Remplissez le volume final après compression V2.
5. Entrez l'exposant polytropique souhaité n=1,2.

6. Appuyez sur le bouton "Polytr.".
Cela calculera et remplira les paramètres p2 et T2 qui satisfont l'exposant polytropique donné n=1,2.
7. Résultats :
Pression finale p2 = 617 kPa
Température finale T2 = 106,8 °C
Travail de pression Wt = 62,2 MJ (17,27 kWh)
Chaleur évacuée vers l'environnement Q = 25,8 MJ
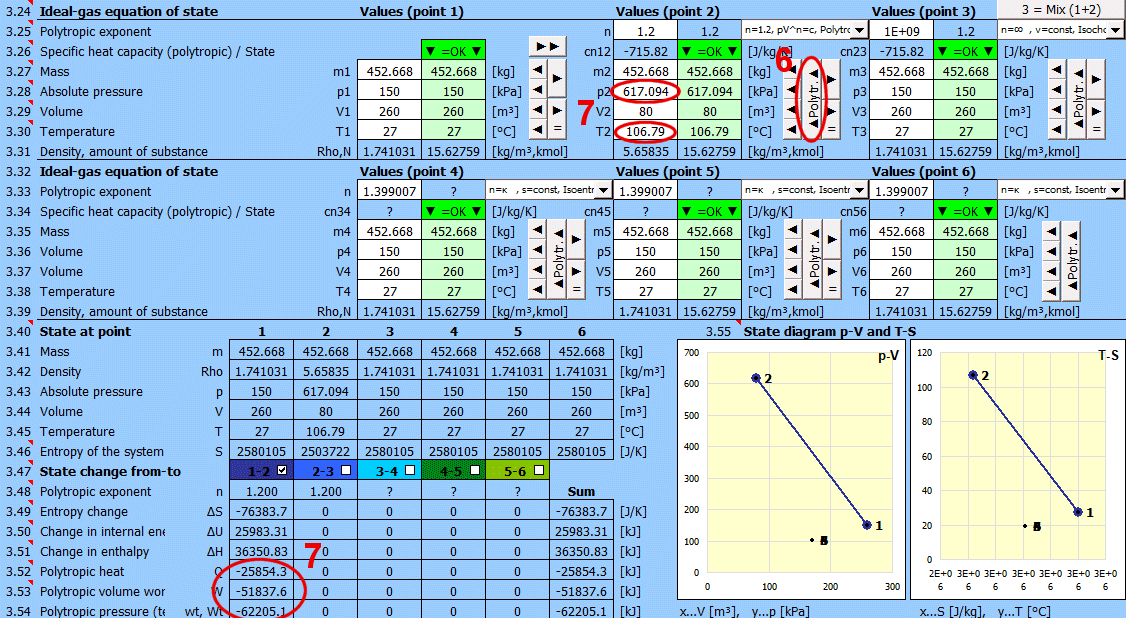
Calcul d'un compresseur à piston (cylindrée 1 litre).
Fluide de travail : Air
Volume de travail : V1 = 0,001 m^3
Exposant polytropique : n=1,3 (Compresseur à piston avec évacuation partielle de
la chaleur, valeur typique pour les compresseurs lents avec refroidissement).
Pression d'aspiration : p1=100 kPa
Pression de refoulement : p2=500 kPa
Température de l'air aspiré : T1=25 °C
Espace mort X : 5% => V3 = 0,00005 m^3 (Pour des raisons de conception, une
expulsion complète du gaz n'est pas possible. Le gaz résiduel se dilate et
réduit le volume du gaz aspiré).
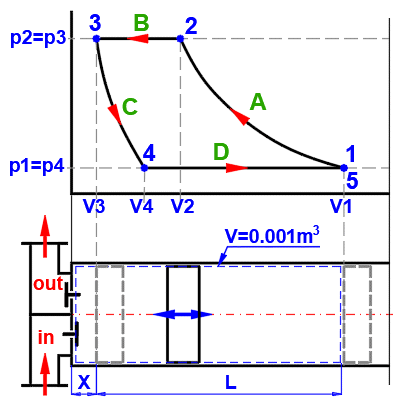
Sélectionnez l'air comme fluide de travail et réglez la température.
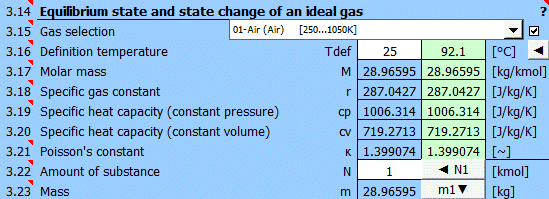
1. Réglez les paramètres au point 1 (p1=100 kPa, V1=0,001 m^3, T1=25 °C),
remplissez m1 à l'aide du bouton "◄".
2. Utilisez le bouton "►►" pour copier les valeurs aux autres points.
3. Entrez la pression de refoulement p2=500 kPa et l'exposant polytropique
n=1,3.
4. Appuyez sur le bouton "Polytr.".
Cela calculera et remplira les paramètres V2 et T2 qui satisfont l'exposant
polytropique donné n=1,3.
5. Copiez les résultats au point 3 à l'aide du bouton "►".
6. Entrez le volume final de refoulement V3 = 0,00005 m^3 et remplissez m3 à
l'aide du bouton "◄".
7. Copiez les résultats au point 4 à l'aide du bouton "►".
8. Entrez la pression d'aspiration p4=100 kPa et l'exposant polytropique n=1,3.
9. Appuyez sur le bouton "Polytr.".
Cela calculera et remplira les paramètres V4 et T4 qui satisfont l'exposant
polytropique donné n=1,3.
Le gaz se dilate jusqu'à l'état p4=p1 (pression d'aspiration).
10. Copiez les résultats au point 5 à l'aide du bouton "►".
11. Entrez le volume final d'aspiration V5 = 0,001 m^3 et remplissez m5 à l'aide
du bouton "◄".
12. Activez l'affichage de l'état dans le diagramme p-V. (Les courbes de
transition sont affichées sous forme de lignes droites).
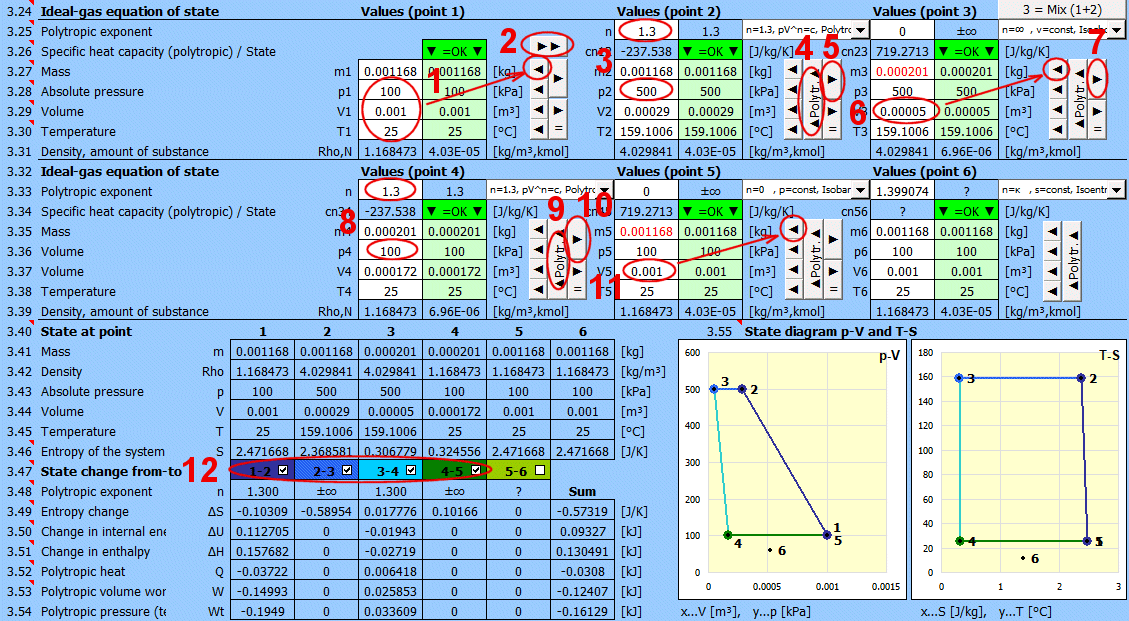
De l'eau s'écoule à travers un tuyau en acier de section circulaire d'un
diamètre intérieur de d=102 mm, d'une épaisseur de paroi de 3 mm et d'une
longueur L=200 m à une température de T1=90 °C et une vitesse de v1=0,1 m/s. Le
tuyau est isolé avec 20 mm de laine minérale, une couche extérieure en PVC de 1
mm d'épaisseur et est peint en blanc. Le tuyau est situé à l'extérieur et exposé
à un flux d'air d'une température de T2=10 °C et d'une vitesse de v2=3 m/s. La
canalisation est exposée au rayonnement solaire avec une intensité de 1000
W/m^2.
Calculez la perte de chaleur et la température de l'eau à l'extrémité du tuyau.
1. Entrez les températures T1 et T2.
2. Sélectionnez le type de paroi.
3. Définissez successivement les couches de paroi (dimensions et propriétés
physiques). Les matériaux peuvent être sélectionnés dans la liste [4.7] et
ajoutés à l'aide du bouton "Add".
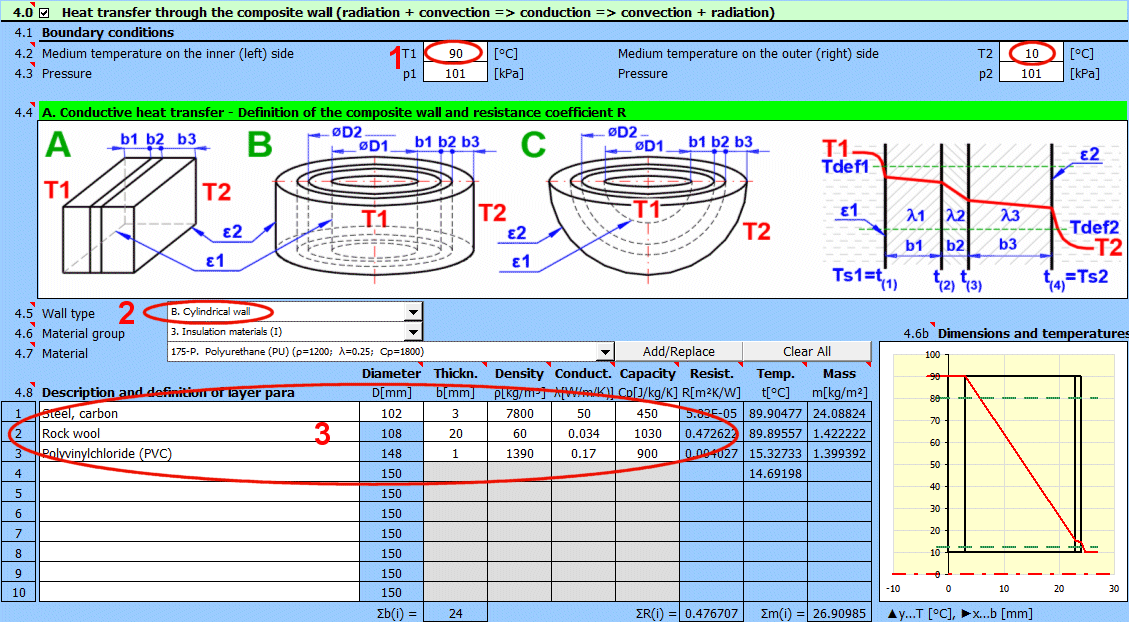
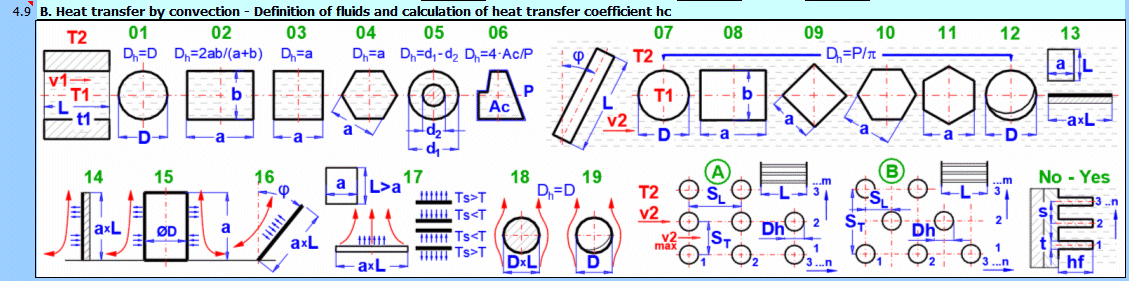
4. Sélectionnez les fluides de travail 1 et 2.
5. Sélectionnez le type d'écoulement = forme de la surface mouillée.
6. Entrez la vitesse d'écoulement et les dimensions.
7. Appuyez sur le bouton pour le calcul itératif des résultats.
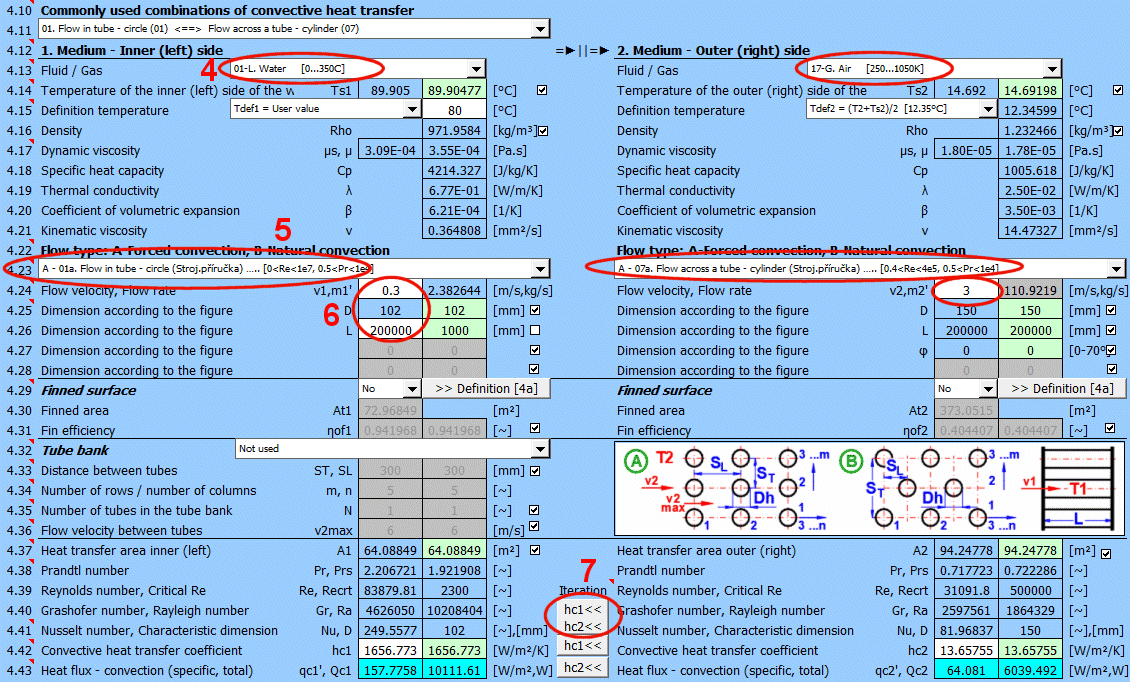
Nous résolvons pour un profil fermé, il n'est donc pas nécessaire de traiter le rayonnement sur la face interne du tuyau (milieu 1).
8. Sélectionnez le type de surface, ou entrez directement l'émissivité ε2 à
[4.45].
9. Sélectionnez le rayonnement thermique vers l'espace.
10. Entrez l'intensité du rayonnement et sélectionnez "* ε" dans la liste
déroulante - l'émissivité de [4.45] est utilisée.
11. Choisissez la taille de la zone irradiée Ai2 par rapport à la zone A2. (Le
soleil n'irradie pas toute la surface du tuyau).
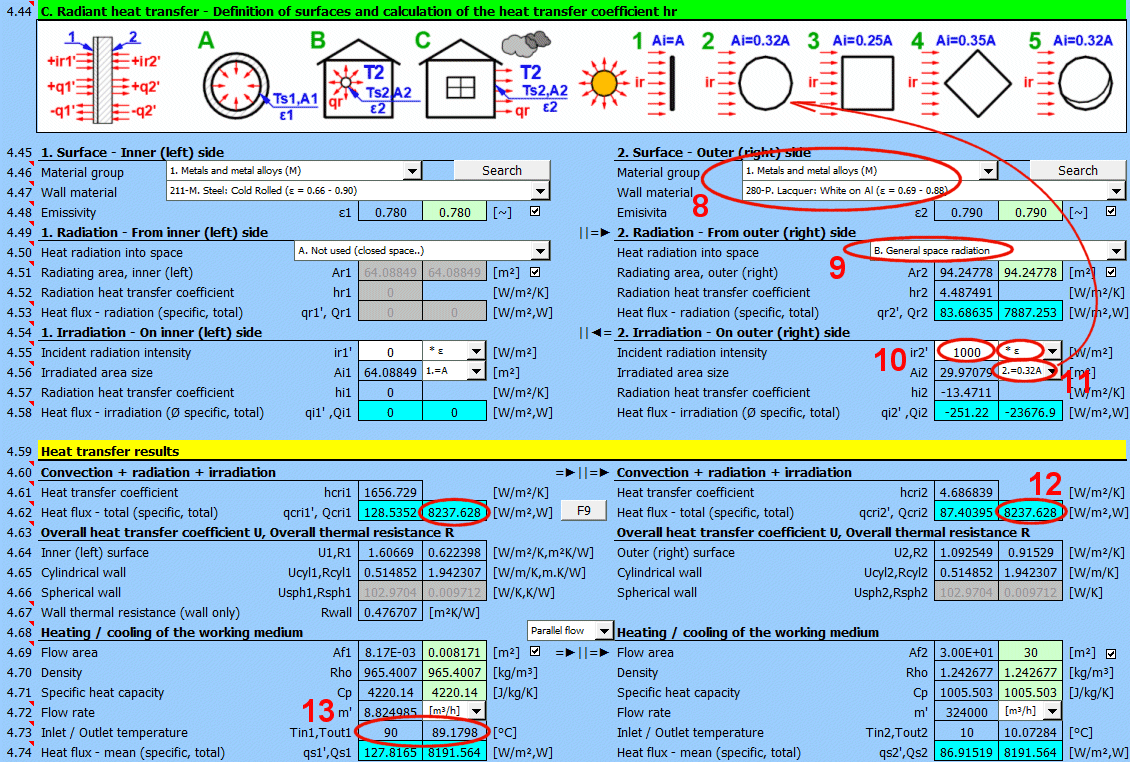
12. Les pertes résultantes sont de 8237 W.
13. La température à l'extrémité de la canalisation est d'environ 89,2 °C.
Essayez de modifier la couche de finition (émissivité ε2 [4.47, 4.48]) à la fois pour le tuyau irradié par le soleil et pour le tuyau non irradié (ir2 = 0 W/m^2 [4.51]).
1. Nommez la solution de transfert de chaleur actuelle.
2. Ajoutez une description de la solution.
3. Ajoutez la solution actuelle à la liste sur la feuille "Walls".
4. Sélectionnez une solution dans la liste des solutions enregistrées.
5. Chargez les données complètes. Les valeurs actuelles seront écrasées par les
valeurs de la solution sélectionnée.

Les solutions sont enregistrées dans la feuille "Walls". Une ligne contient
une solution enregistrée.
La feuille "Walls" est librement accessible et peut être éditée normalement à
l'aide des outils Excel (par exemple, suppression des solutions inutiles -
lignes).
Si vous avez besoin de récupérer une valeur spécifique et de l'utiliser dans votre propre formule, la fonction `GetWallProp` est disponible.
Syntaxe :
`GetWallProp(ID;valuename)`
`ID` ... Numéro de ligne sur la feuille "Walls" contenant la solution
enregistrée.
`valuename` ... Nom de la valeur que vous souhaitez récupérer.
Exemple :
`=GetWallProp(1;"Date")` ... Renvoie la date à laquelle la solution a été
ajoutée à la liste.
`=GetWallProp(1;"T1")` ... Renvoie la température du fluide 1 - T1 en [°C].
`=GetWallProp(1;"U1")` ... Renvoie la valeur du coefficient global de transfert
de chaleur U1 en [W/m²/K].
Une tâche courante peut être de déterminer les paramètres de transfert de chaleur si vous connaissez (par exemple, à partir de mesures) certaines valeurs et que vous ne souhaitez pas résoudre le transfert de chaleur complet à travers la paroi.
La température d'un mur périphérique de maison de 3,5 m de hauteur et 20 m de long a été mesurée avec une caméra thermique à Ts1=3 °C. L'air ambiant a une température de T1=0 °C et s'écoule le long du mur à une vitesse de 3 m/s.
Déterminez le coefficient global de transfert de chaleur U et le flux thermique total Q.
1. Entrez la température de l'air en circulation T1=0 °C (La température T2
peut être choisie arbitrairement).
2. Sélectionnez une paroi plane.
3. Choisissez un matériau de paroi (ses paramètres n'ont pas d'importance).
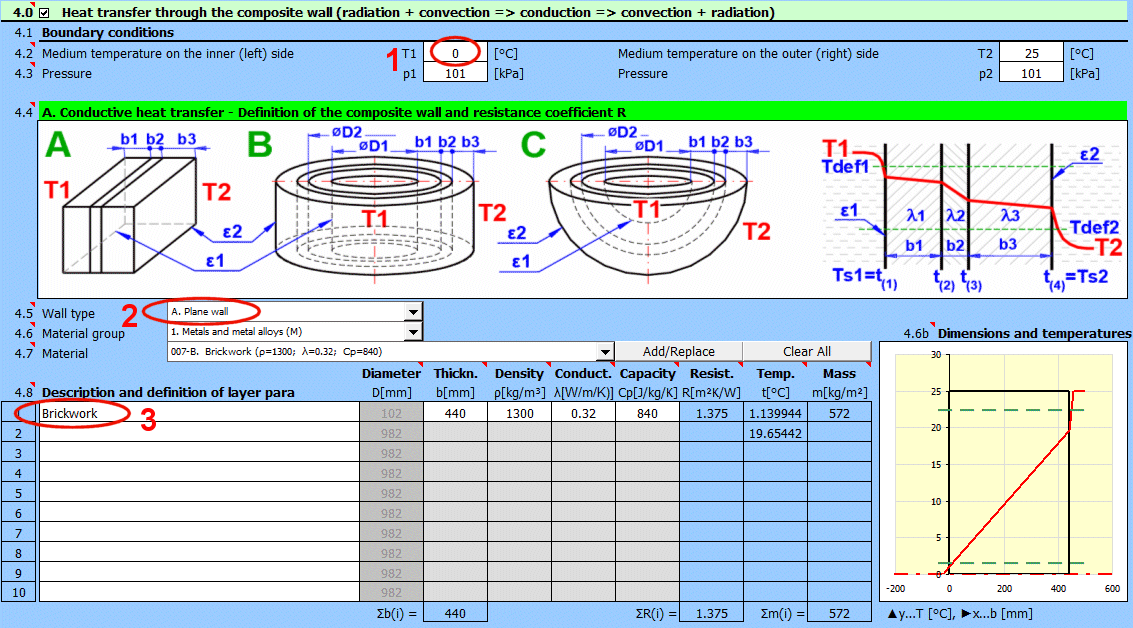
4. Sélectionnez l'air comme fluide de travail.
5. Décochez le remplissage automatique de la température de la paroi Ts1. Cela
interrompra le calcul complexe et seule la partie gauche de la paroi sera
résolue.
6. Entrez la température de la paroi Ts1=3 °C.
7. Sélectionnez l'écoulement forcé autour d'une surface plane.
8. Entrez la vitesse d'écoulement v1=3 m/s.
9. Entrez les dimensions de la surface.
10. Appuyez sur le bouton pour itérer hc1.
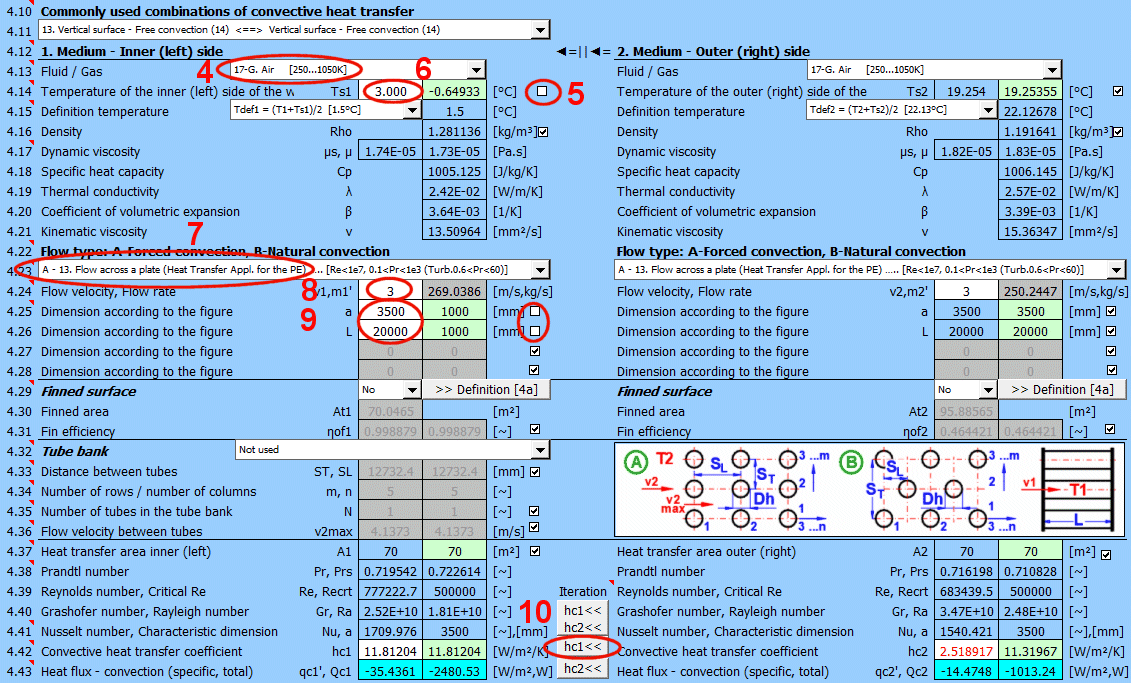
11. Choisissez le matériau de surface de la paroi.
12. Ou entrez directement l'émissivité de la surface.
13. Sélectionnez le rayonnement thermique extérieur.
14. Vous obtiendrez le flux thermique total à travers la paroi Q1 et le
coefficient global de transfert de chaleur U1.
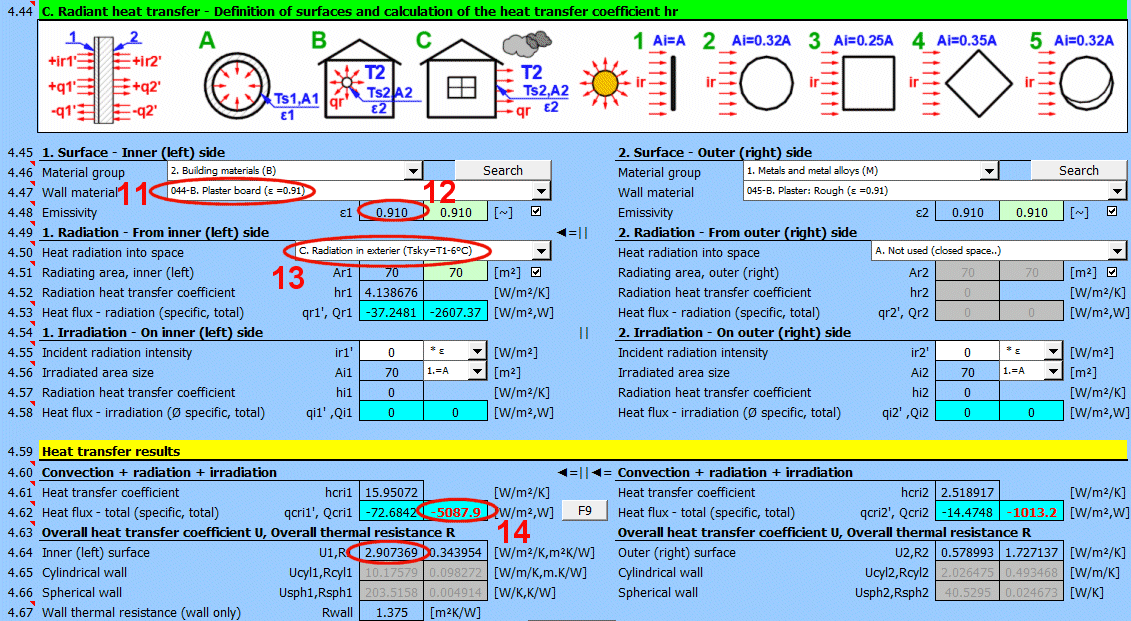
Essayez de modifier la couche de finition (émissivité ε2 [4.47, 4.48]).
Pour divers réservoirs cryogéniques, thermos, etc., une paroi avec un vide d'un côté est souvent utilisée.
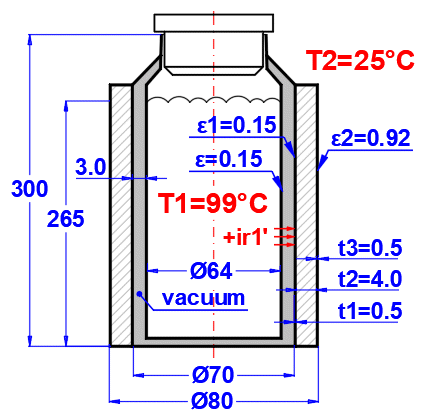
Une thermos d'un volume de 0,85 L a une paroi cylindrique composée d'une tôle d'acier de t1=0,5 mm, d'une isolation de t2=4,0 mm et d'un revêtement en PVC de t3=0,5 mm. Il y a un vide sur la face intérieure de la paroi. Sur la face extérieure, il y a de l'air à une température de 25 °C. La paroi cylindrique a un diamètre intérieur D=70 mm et une hauteur L=300 mm. À l'intérieur de la thermos se trouve un récipient avec de l'eau à une température de 99 °C. L'épaisseur du vide est de 3 mm. Le rayonnement vers la paroi intérieure est de 45 W/m^2 (d'après le calcul dans la section [7.0]).
Déterminez le coefficient global de transfert de chaleur U et le flux thermique total Q.
Simplification acceptée : Le transfert de chaleur de la paroi périphérique est résolu ; l'influence du fond est compensée par l'utilisation d'une hauteur de 300 mm.
1. Entrez les températures T1=99 °C et T2=25 °C.
2. Sélectionnez une paroi cylindrique.
3. Définissez les différentes couches de paroi.
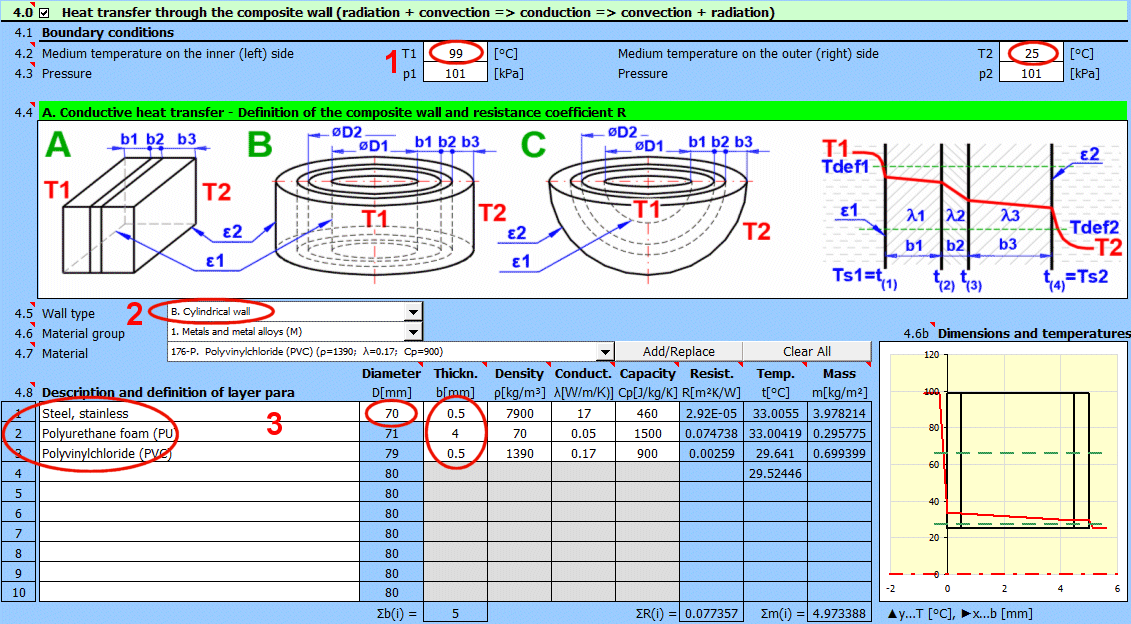

4. Sélectionnez les fluides de travail 1 et 2.
5. Sélectionnez le type d'écoulement = forme de la surface mouillée.
6. Entrez les dimensions du récipient mouillé.
7. Appuyez sur le bouton pour le calcul itératif des résultats.
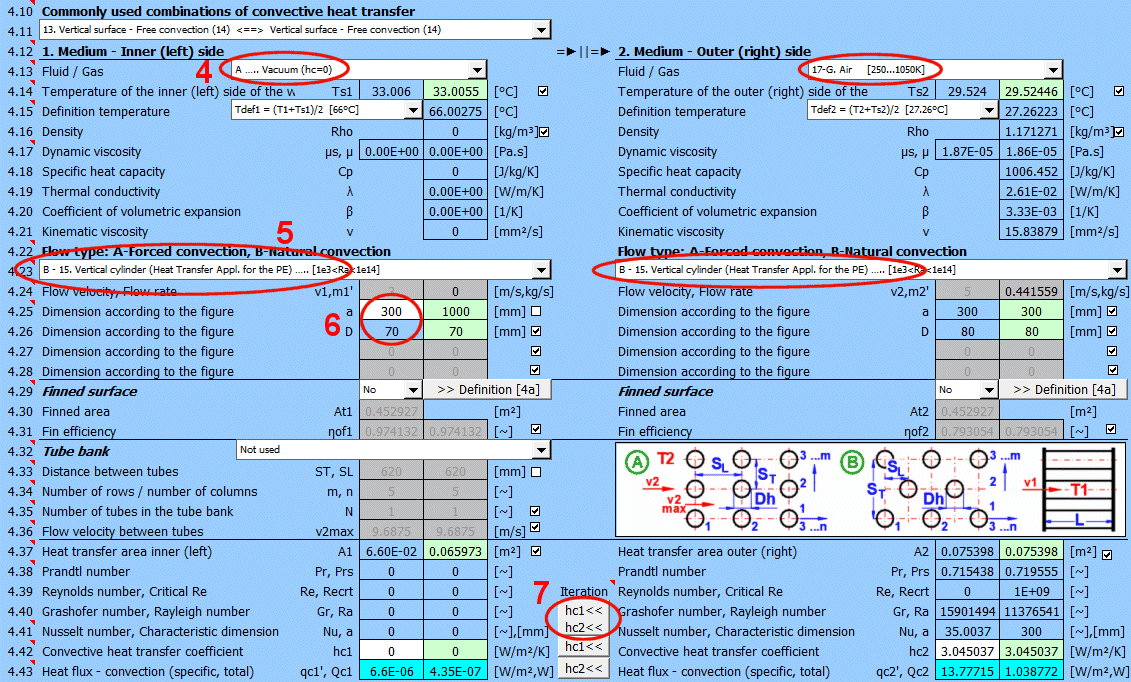
Il est nécessaire de résoudre le rayonnement vers l'espace pour la surface
extérieure.
8. Sélectionnez le type de surface, ou entrez directement l'émissivité ε2=0,92 à
[4.45].
9. Sélectionnez le rayonnement thermique intérieur.
Irradiation de la surface intérieure de la paroi.
10. Le rayonnement vers l'espace n'est pas résolu - un espace fermé est traité.
11. Dans la section [7.0], l'intensité du rayonnement ir1=45 W/m^2 est calculée
(Exemple 18 ci-dessous) pour une émissivité de paroi ε1=0,15, donc choisissez un
multiplicateur de "* 1".
12. Toute la surface intérieure est irradiée, sélectionnez l'option "1.=A".
13. Les valeurs q, Q et U peuvent être utilisées dans des calculs ultérieurs
(Exemple 15 ci-dessous).
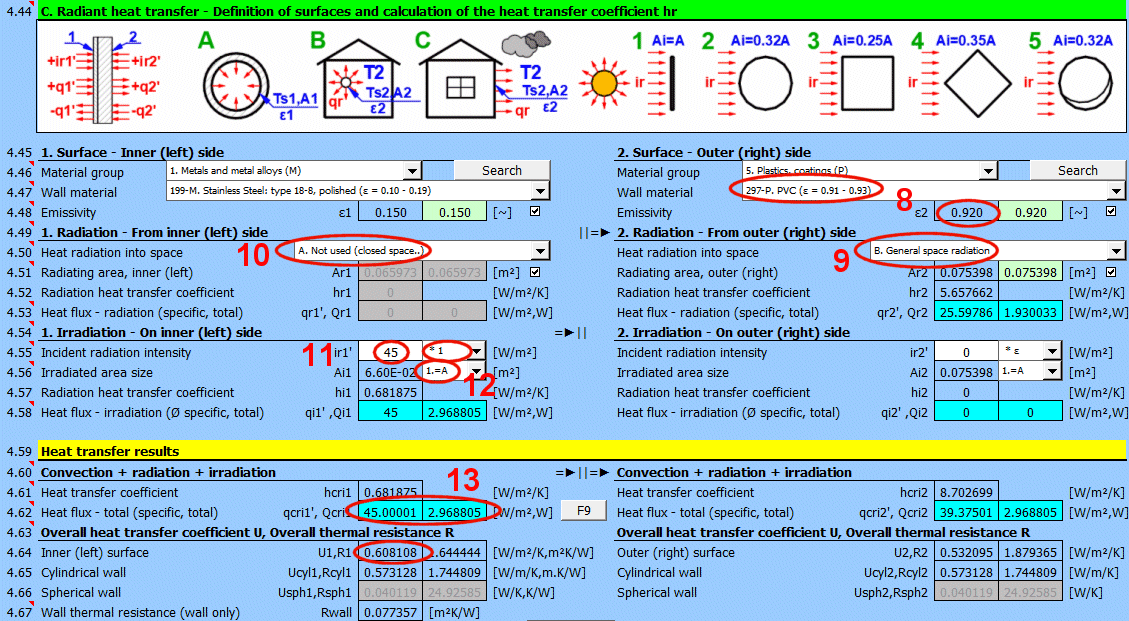
Analyse d'un générateur électrique avec des modules TEG et un refroidisseur à air.
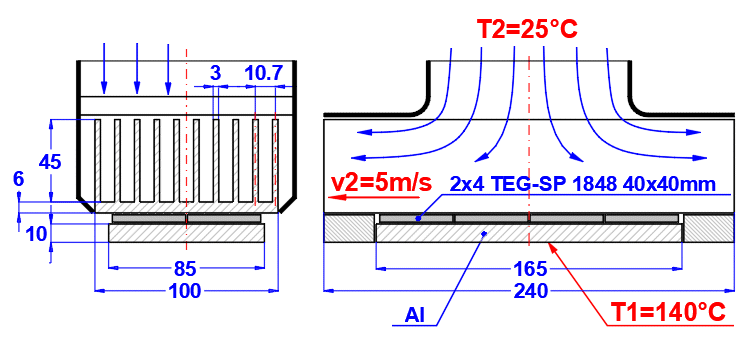
Huit modules TEG sont fixés d'un côté à une plaque d'aluminium de dimensions 85 x 165 x 10 mm. De l'autre côté, ils sont fixés à un dissipateur thermique en aluminium de dimensions 100 x 240 x 51 mm avec dix ailettes et une épaisseur de base de 6 mm. La plaque d'aluminium est en contact avec une source de chaleur à une température de T1=140 °C. L'air circule à travers le dissipateur thermique à une température de T2=25 °C avec une vitesse de 5 m/s. La conductivité thermique du module TEG est de 1,5 [W/m/K].
Déterminez la température du module TEG sur les côtés chaud et froid.
1. Entrez les températures T1=140 °C et T2=25 °C.
2. Sélectionnez une paroi plane.
3. Définissez les différentes couches de paroi selon la figure.
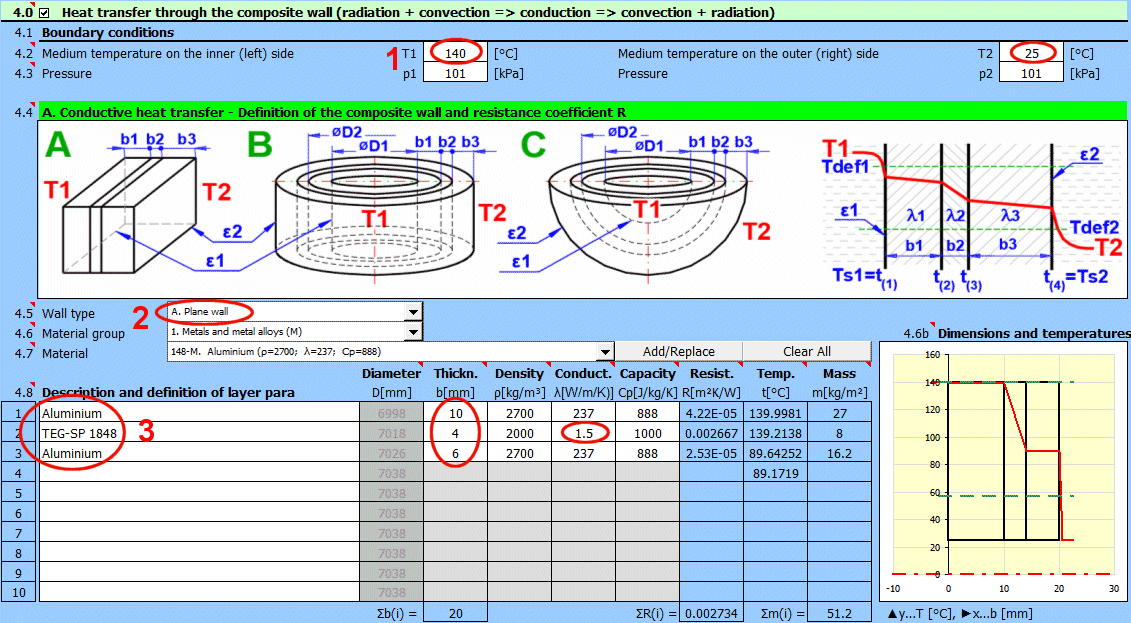

4. Sélectionnez les fluides de travail 1 et 2 (Fluide 1 - connexion de
contact à la source de chaleur).
5. Entrez les dimensions de la plaque de contact.
6. Sélectionnez le type d'écoulement (Écoulement forcé autour d'une plaque =
écoulement d'air dans le refroidisseur).
7. Entrez les dimensions de la base du refroidisseur et la vitesse d'écoulement
de l'air.
8. Activez l'utilisation d'une surface ailetée et définissez ses dimensions dans
la section [4a.0].
9. Après avoir défini les dimensions des ailettes, appuyez sur le bouton pour le
calcul itératif des résultats.
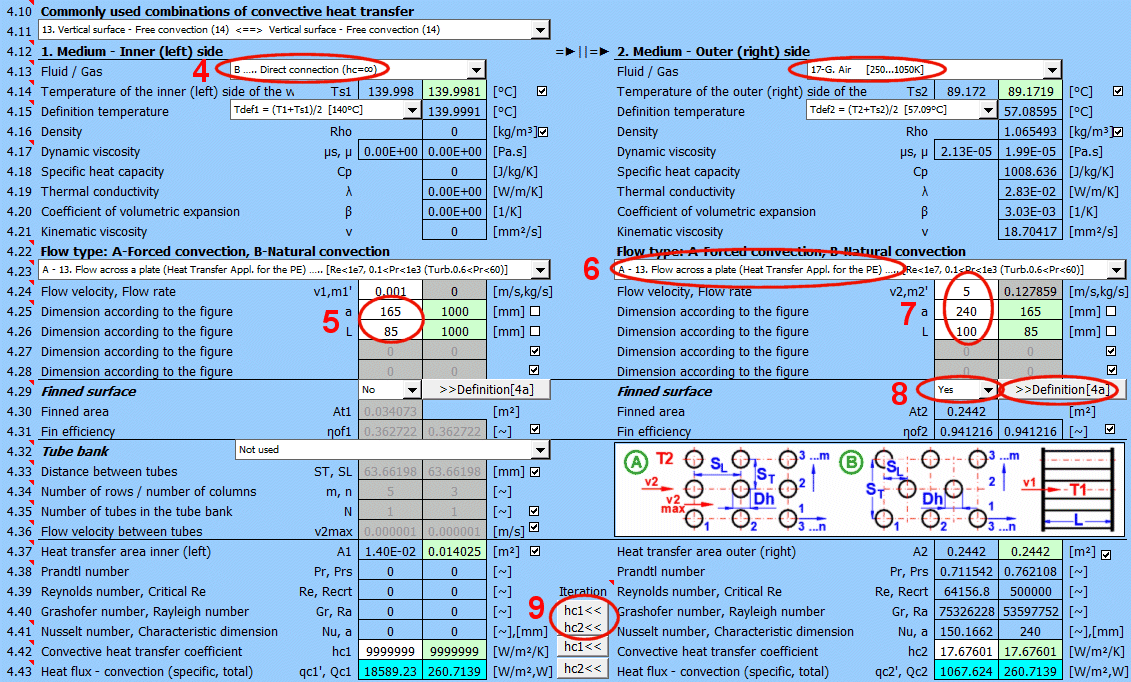
10. Choisissez la forme rectangulaire de l'ailette.
11. Entrez les dimensions et le nombre d'ailettes. Le nombre suggéré d'ailettes
est calculé à partir de la largeur du champ d'ailettes [4a.5] et des distances
entre les ailettes [4a.9].
12. Le rendement des ailettes est calculé (utilisé pour calculer le coefficient
de transfert de chaleur [4.29, 4.39]).
13. La surface mouillée, qui est augmentée par les ailettes, est calculée et
utilisée à la place de la valeur d'origine [4.34].
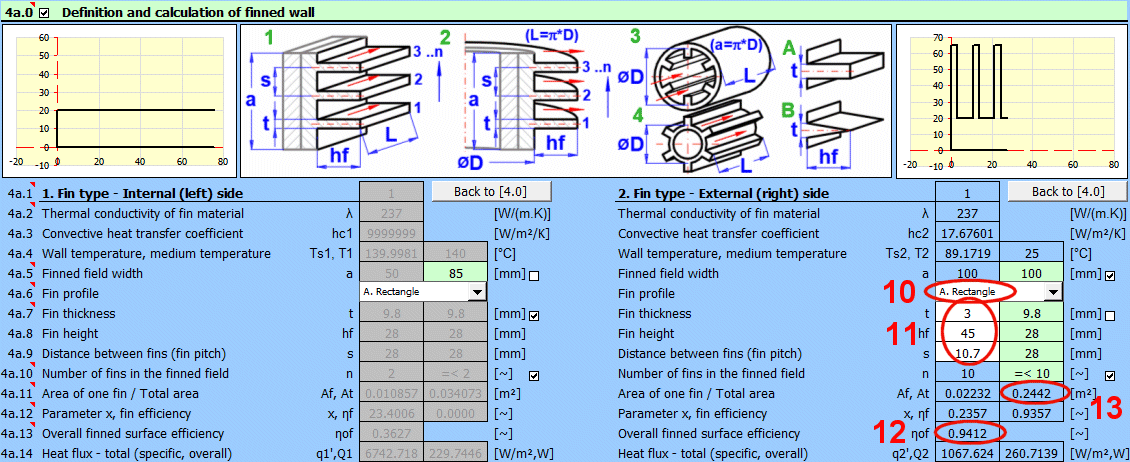
Dans ce calcul, il n'est pas nécessaire de prendre en compte le rayonnement ; les paramètres doivent être réglés en conséquence.
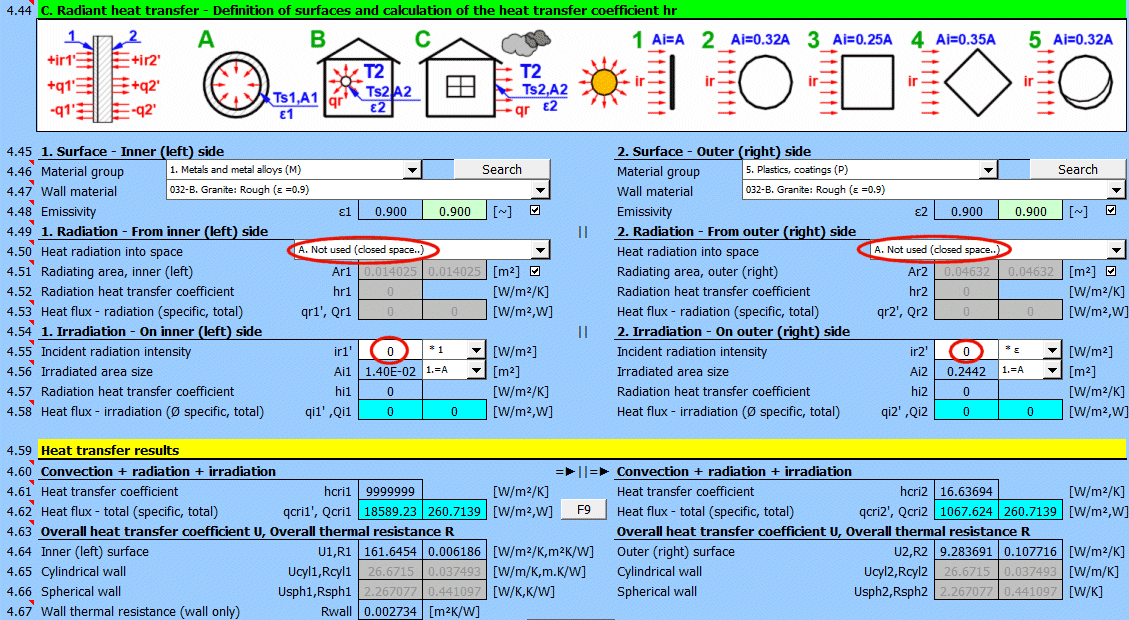
Les résultats requis (températures des parois du module TEG) se trouvent dans le tableau [4.8].
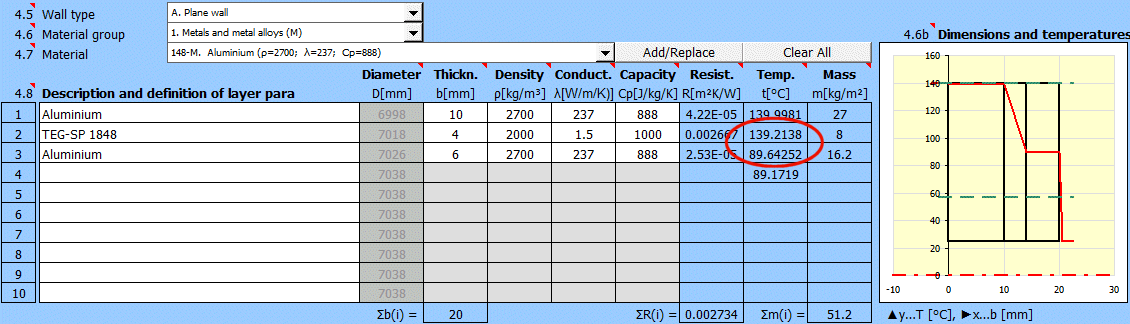
Conclusion : La différence de température est de 50 °C. Selon les données du catalogue, pour cette différence de température, la puissance d'un seul module est d'environ 1 W, soit 8 W pour 8 modules. Pour augmenter la différence de température, il serait nécessaire d'augmenter significativement la surface du dissipateur thermique (plus d'ailettes fines et hautes) ou d'utiliser, par exemple, un refroidissement par eau.
Calcul du transfert de chaleur dans un faisceau de tubes.
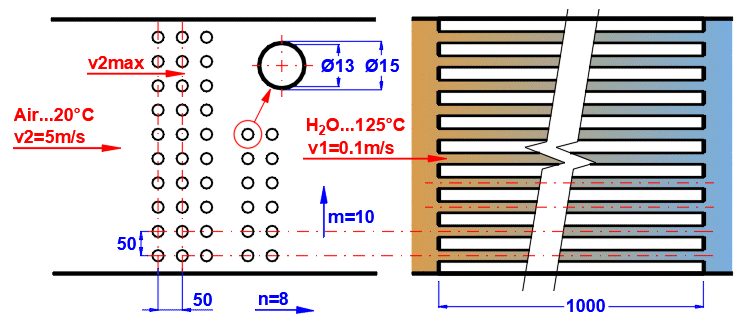
De l'eau provenant d'un puits géothermique à une température de T1=125 °C s'écoule à travers les tubes à une vitesse de 0,1 m/s. Les tubes en acier sont disposés en faisceau de 10 rangées, 8 colonnes. Le diamètre intérieur du tube est D1=13 mm, le diamètre extérieur D2=15 mm. L'air entre dans le faisceau de tubes à une température de T2=20 °C à une vitesse de 5 m/s.
Déterminez la température de sortie de l'air et la puissance de l'échangeur de chaleur.
1. Entrez les températures T1=125 °C et T2=20 °C.
2. Sélectionnez une paroi cylindrique.
3. Définissez les dimensions et le matériau du tube.
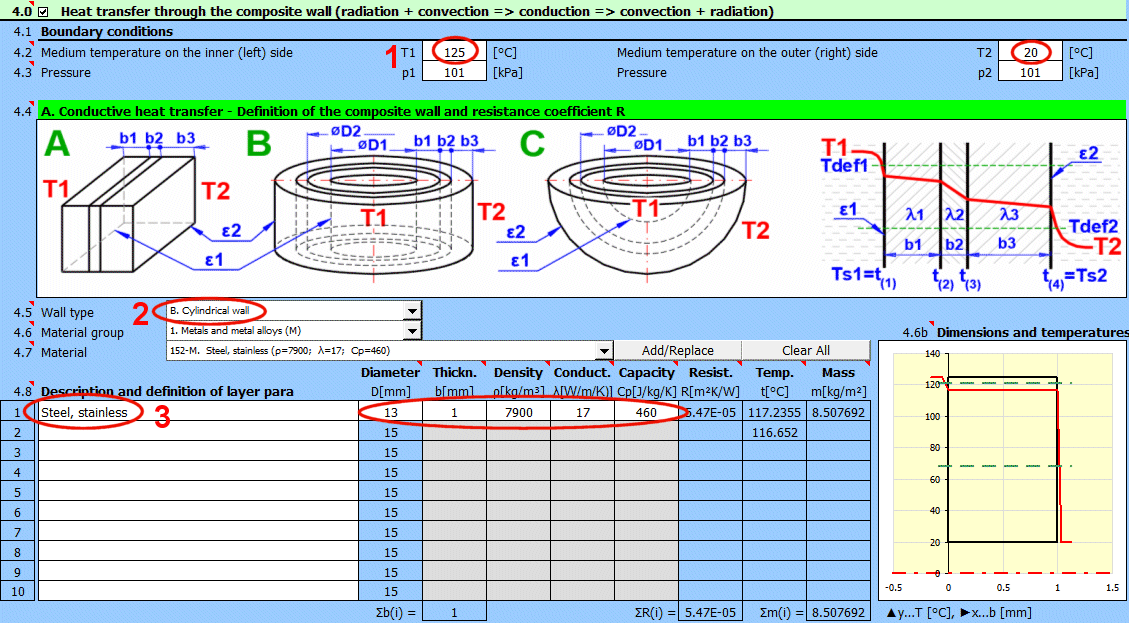

4. Sélectionnez les fluides de travail 1 et 2.
5. Sélectionnez le type d'écoulement (L'eau s'écoule à travers le tube, l'air
s'écoule autour du tube).
6. Entrez les vitesses d'écoulement et les dimensions intérieures et extérieures
du tube.
7. Activez et sélectionnez la disposition des tubes dans le faisceau.
8. Entrez les distances entre les tubes et leur nombre selon la figure.
9. Après avoir défini les dimensions, appuyez sur le bouton pour le calcul
itératif des résultats.
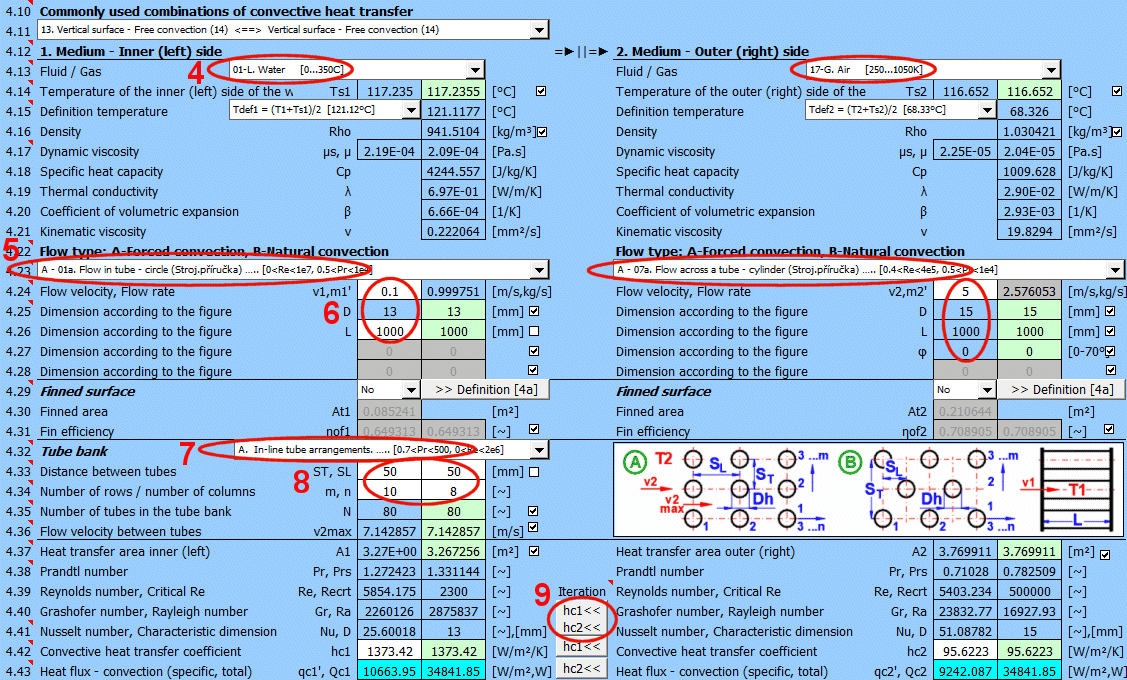
Dans ce calcul, il n'est pas nécessaire de prendre en compte le rayonnement ; les paramètres doivent être réglés en conséquence.
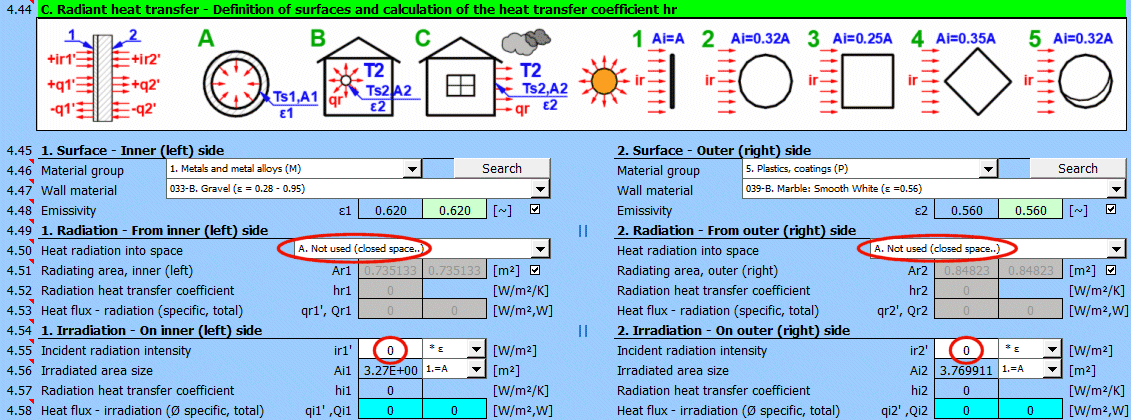
10. Sélectionnez le type d'écoulement mutuel - Contre-courant (Plus d'options
sont disponibles dans le chapitre Échangeurs de Chaleur).
11. Lorsque la case est cochée, les valeurs prédéfinies pour Af, Rho, Cp sont
utilisées. Le programme essaie de les suggérer en fonction des valeurs saisies
ci-dessus.
12. Si les valeurs prédéfinies ne vous conviennent pas, vous pouvez, après avoir
décoché la case (11), saisir vos propres valeurs.
13. La température de sortie de l'air est de 30,5 °C et la puissance est d'un
peu moins de 32 kW.
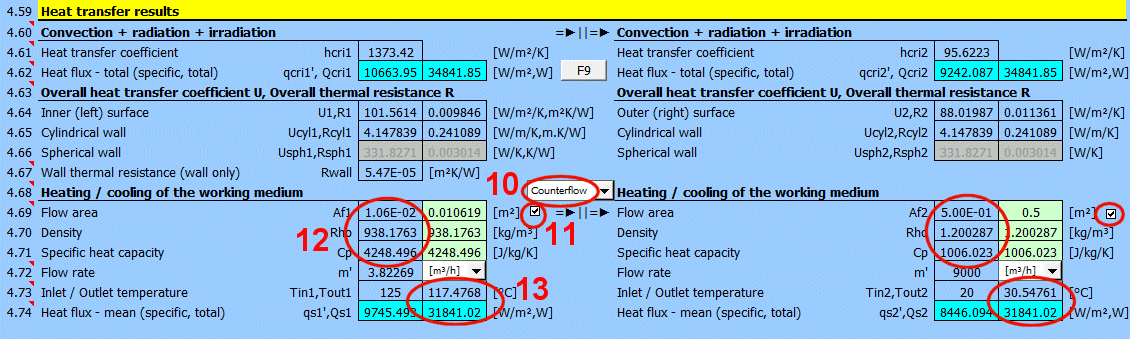
Conclusion : L'augmentation de la température de l'air de 10 °C est relativement faible. Pour un échangeur de chaleur eau-air, il serait clairement plus avantageux d'utiliser des ailettes.
Dans l'exemple précédent, des tubes sans ailettes ont été utilisés. Dans cet exemple, nous utiliserons moins de tubes de plus grande dimension et avec des ailettes.
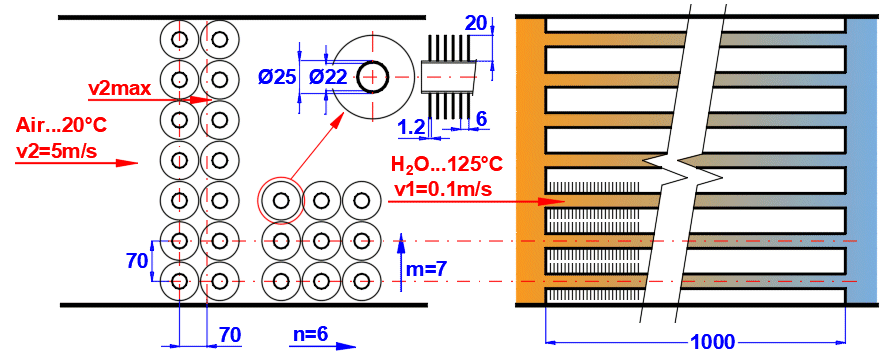
De l'eau provenant d'un puits géothermique à une température de T1=125 °C s'écoule à travers les tubes à une vitesse de 0,1 m/s. Les tubes en acier sont disposés en faisceau de 7 rangées, 6 colonnes. Le diamètre intérieur du tube est D1=22 mm, le diamètre extérieur D2=25 mm. L'air entre dans le faisceau de tubes à une température de T2=20 °C à une vitesse de 5 m/s. Les tubes sont équipés d'ailettes. Épaisseur de l'ailette t=1,2 mm, hauteur de l'ailette hf=20 mm et pas s=6 mm. Le nombre maximum d'ailettes n=167 est utilisé.
Déterminez la température de sortie de l'air et la puissance de l'échangeur de chaleur.
1. Entrez les températures T1=125 °C et T2=20 °C.
2. Sélectionnez une paroi cylindrique.
3. Définissez les dimensions et le matériau du tube.
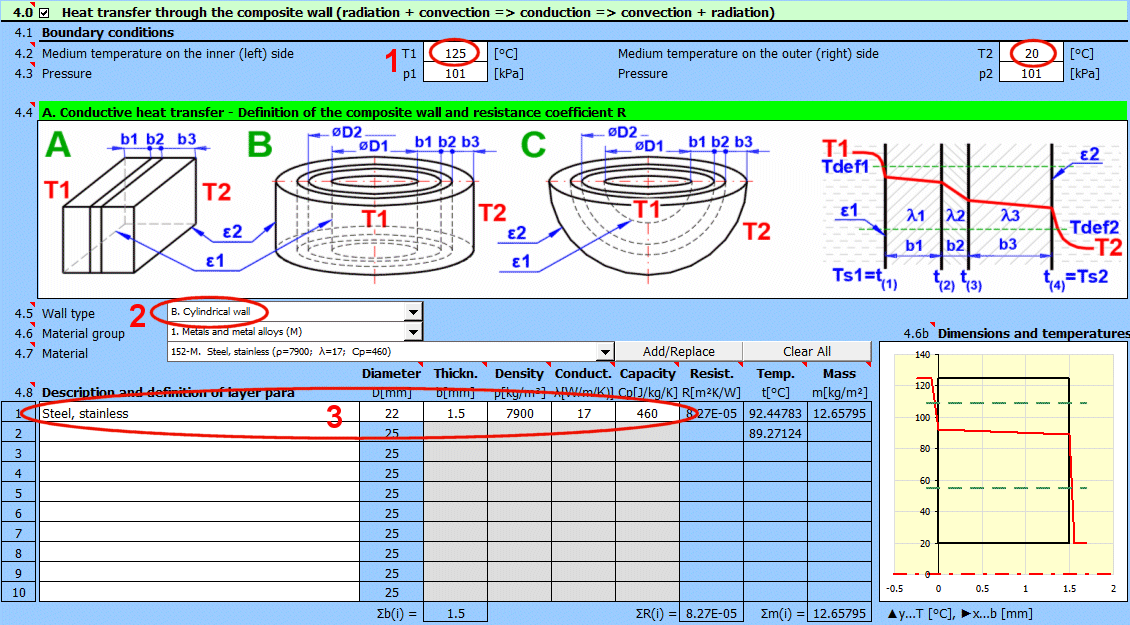

4. Sélectionnez les fluides de travail 1 et 2.
5. Sélectionnez le type d'écoulement (L'eau s'écoule à travers le tube, l'air
s'écoule autour du tube).
6. Entrez les vitesses d'écoulement et les dimensions intérieures et extérieures
du tube.
7. Activez l'utilisation d'une surface ailetée et définissez ses dimensions dans
la section [4a.0].
8. Activez et sélectionnez la disposition des tubes dans le faisceau.
9. Entrez les distances entre les tubes et leur nombre selon la figure.
10. Après avoir défini les dimensions, appuyez sur le bouton pour le calcul
itératif des résultats.
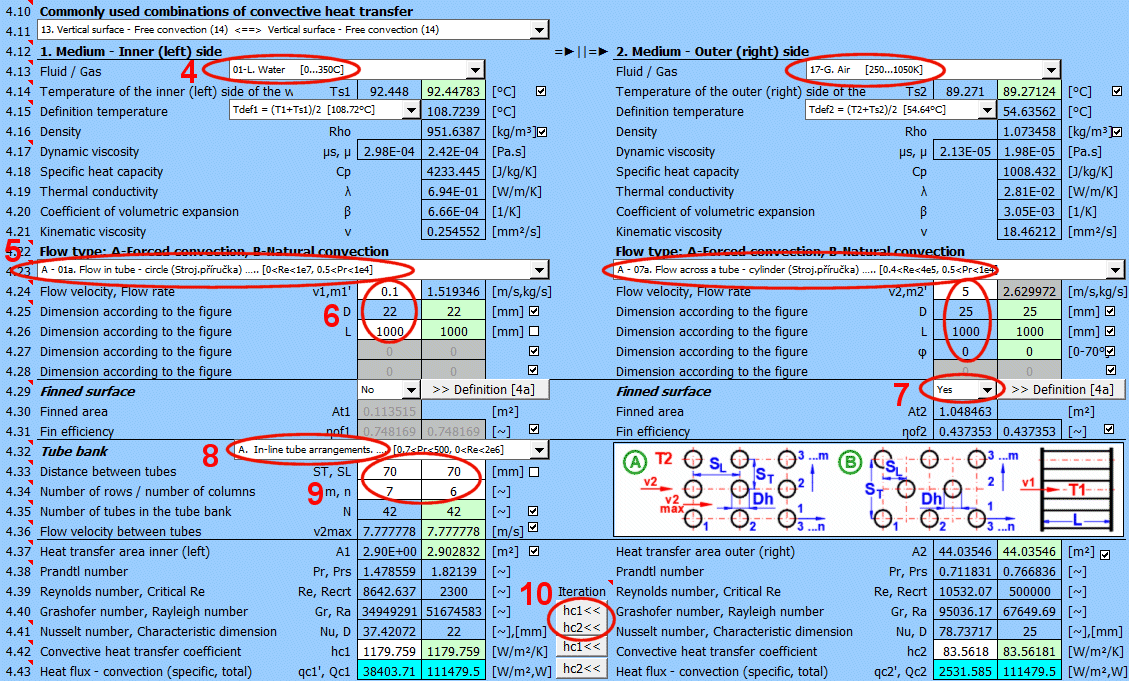
11. Choisissez la forme rectangulaire de l'ailette.
12. Entrez les dimensions et le nombre d'ailettes. Le nombre suggéré d'ailettes
est calculé à partir de la largeur du champ d'ailettes [4a.5] et des distances
entre les ailettes [4a.9].
13. Le rendement des ailettes est calculé (utilisé pour calculer le coefficient
de transfert de chaleur [4.29, 4.39]).
14. La surface mouillée, qui est augmentée par les ailettes, est calculée et
utilisée à la place de la valeur d'origine [4.34].
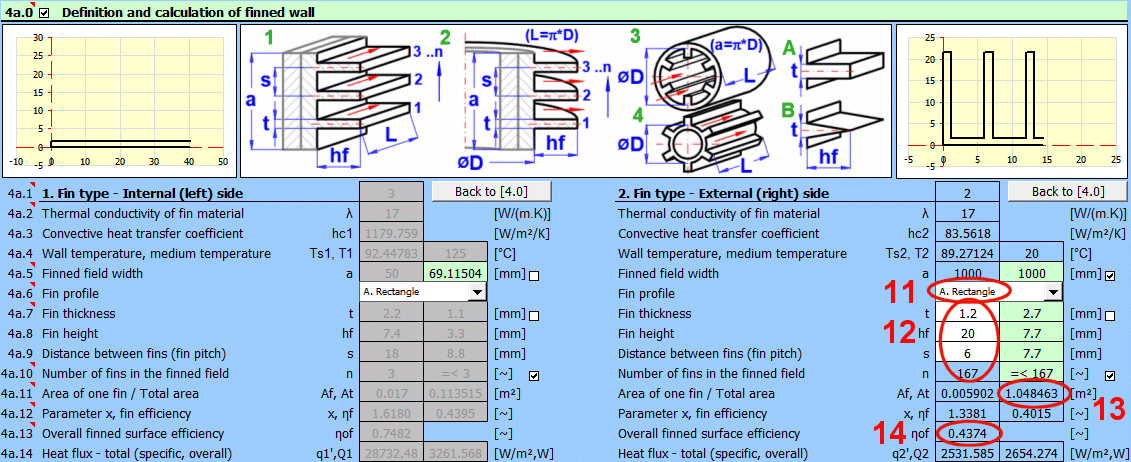
Dans ce calcul, il n'est pas nécessaire de prendre en compte le rayonnement ; les paramètres doivent être réglés en conséquence.
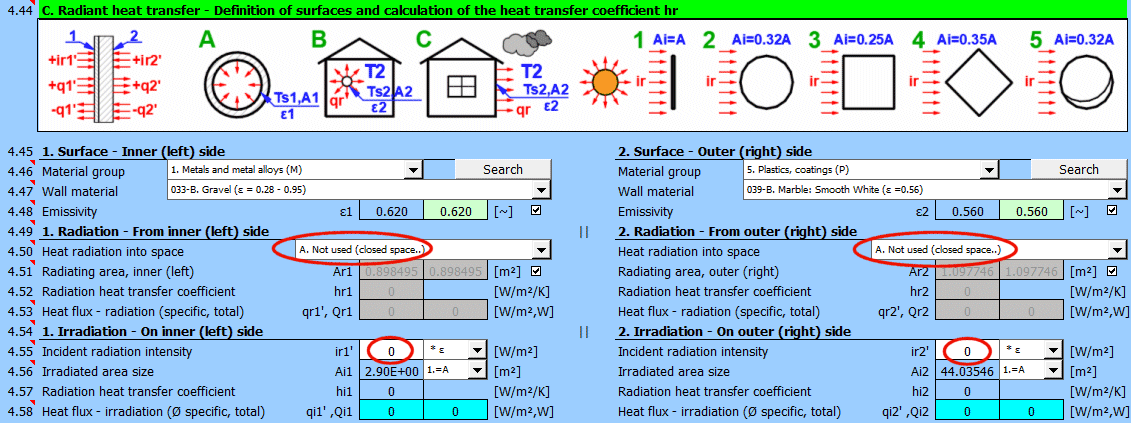
15. Sélectionnez le type d'écoulement mutuel - Contre-courant (Plus d'options
sont disponibles dans le chapitre Échangeurs de Chaleur).
16. Lorsque la case est cochée, les valeurs prédéfinies pour Af, Rho, Cp sont
utilisées. Le programme essaie de les suggérer en fonction des valeurs saisies
ci-dessus.
17. Si les valeurs prédéfinies ne vous conviennent pas, vous pouvez, après avoir
décoché la case (16), saisir vos propres valeurs.
18. La température de sortie de l'air est de 49,8 °C et la puissance 88 kW.
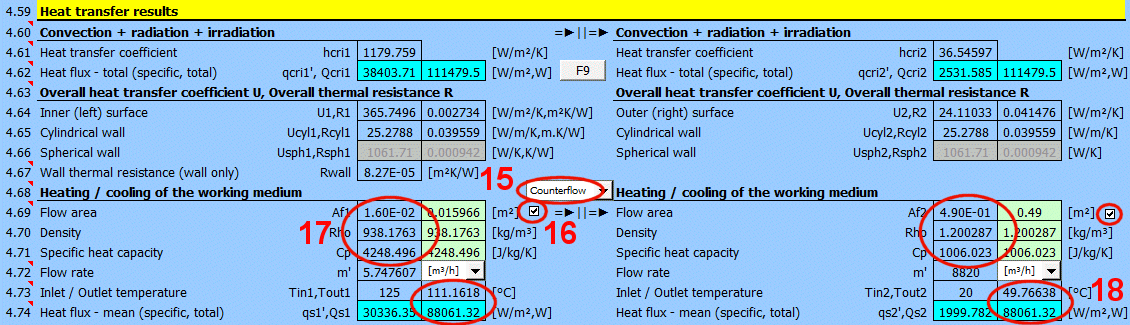
Conclusion : L'augmentation de la température de l'air de 30 °C est le triple de celle de l'exemple précédent, avec un nombre de tubes divisé par deux.
D'après l'exemple 11, nous connaissons le coefficient global de transfert de chaleur U=0,6081 [W/m²/K] et la surface intérieure A=0,0659 [m²]. La température initiale du liquide (eau) T1s=99 °C. La température ambiante T2=25 °C. La masse du liquide est de 0,85 kg.

Déterminez le temps de refroidissement du liquide de la température T1s=99 °C à la température T1e=39 °C.
1. Sélectionnez le liquide dans la liste. Si le liquide n'est pas dans la
liste, décochez la case et entrez la valeur de Cp.
2. Cochez / décochez la case. Si cochée, les valeurs actuelles de la section
[4.0] sont utilisées.
3. Remplissez les valeurs d'entrée requises.
4. Le temps de refroidissement à 39 °C est de 41,5 heures. Cela correspond aux
tests utilisateur des thermos de milieu de gamme.
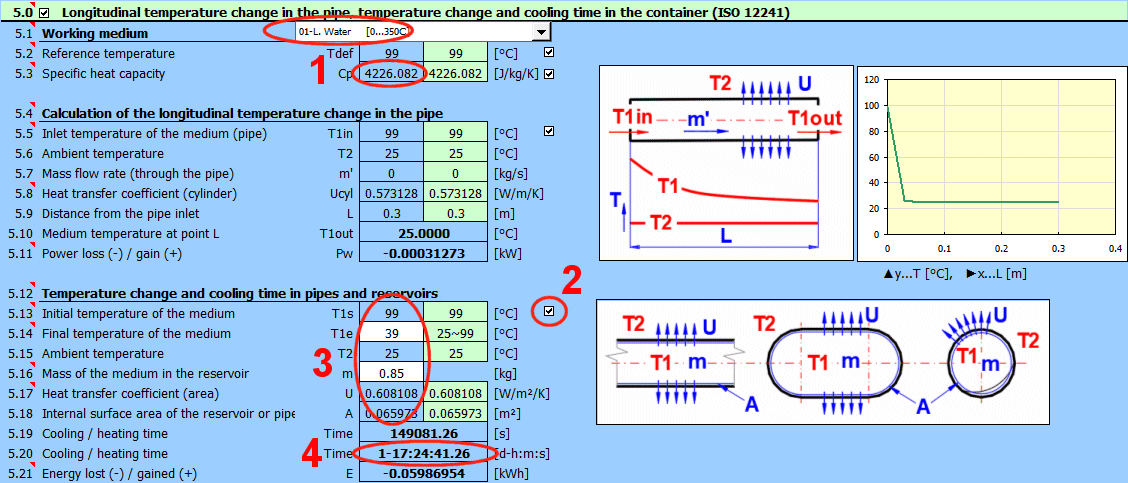
Un échangeur de chaleur tubulaire est utilisé pour le refroidissement de l'huile. Le débit massique de l'eau de refroidissement dans le tube intérieur est m1'=0,25 kg/s, le débit massique de l'huile dans la section annulaire extérieure est m2'=0,15 kg/s. L'eau entre dans l'échangeur de chaleur à une température de T1in=20 °C, l'huile à une température de T2in=98 °C. Le coefficient global de transfert de chaleur pour la paroi cylindrique est de 3,25 W/m/K.
Une température de sortie de l'huile T2Out=62 °C est requise. Déterminez la température de sortie de l'eau et la longueur de l'échangeur de chaleur pour un échangeur de chaleur tubulaire à contre-courant.
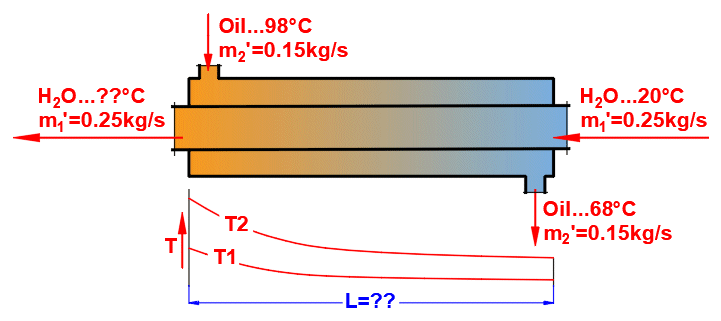

1. Sélectionnez le type d'échangeur de chaleur.
2. Si vous décidez de charger des données à partir de la définition de la paroi
dans la section [4.0], sélectionnez la définition appropriée et chargez avec le
bouton "Load".
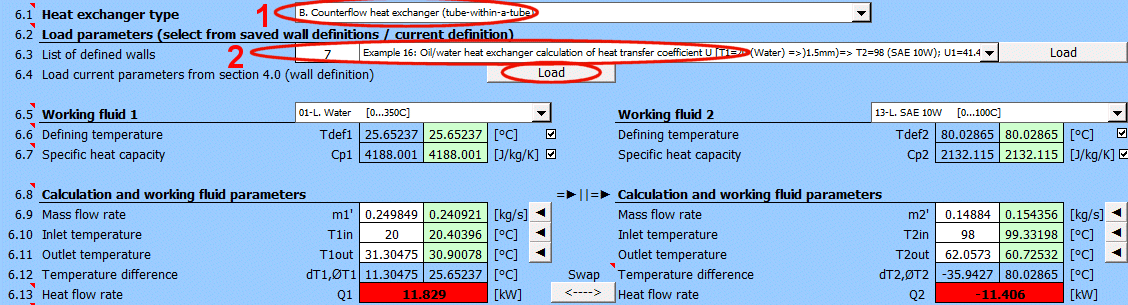
3. Sélectionnez les fluides de travail 1 et 2. Si non dans la liste, entrez
directement la valeur de Cp [6.7].
4. Entrez les paramètres du fluide 1.
5. Entrez les paramètres du fluide 2.
Les valeurs Q1 et Q2 [6.13] seront très probablement différentes et marquées en
rouge. Il est nécessaire de résoudre le bilan énergétique. Dans les champs verts
se trouvent les valeurs calculées qui, lorsqu'elles sont utilisées, garantissent
que Q1=-Q2.
6. Appuyez sur le bouton qui transfère la valeur de conception à T1Out. La
température de sortie de l'eau T1Out=31 °C.
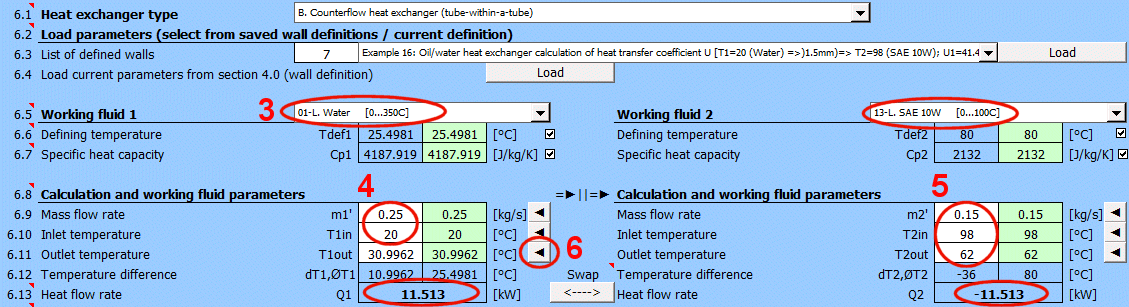
Après avoir résolu le bilan énergétique, il est possible de calculer la longueur du tube (ou la surface).
7. Sélectionnez le type de calcul B. Dans ce cas, vous calculez la longueur de
l'échangeur de chaleur et vous connaissez Ucyl [W/m/K].
8. Entrez la valeur du coefficient global de transfert de chaleur pour le tube
Ucyl. Si vous avez chargé des valeurs du calcul de la paroi (2), cette valeur se
trouve dans le champ vert.
9. Le résultat du calcul de la longueur est L=66 m.
10. Si vous connaissez le diamètre du tube, vous pouvez convertir la longueur en
surface d'échange thermique.
11. Si vous souhaitez inclure l'encrassement de l'échangeur de chaleur pendant
le fonctionnement dans le calcul, entrez le coefficient d'encrassement Rf et
réduisez la valeur de Ucyl [6.21] de 4% [6.36].
12. Utilisez le bouton "▲U" pour régler la valeur corrigée de Ucyl. La longueur
du tube pour l'échangeur de chaleur incluant l'encrassement est alors L=69 m.
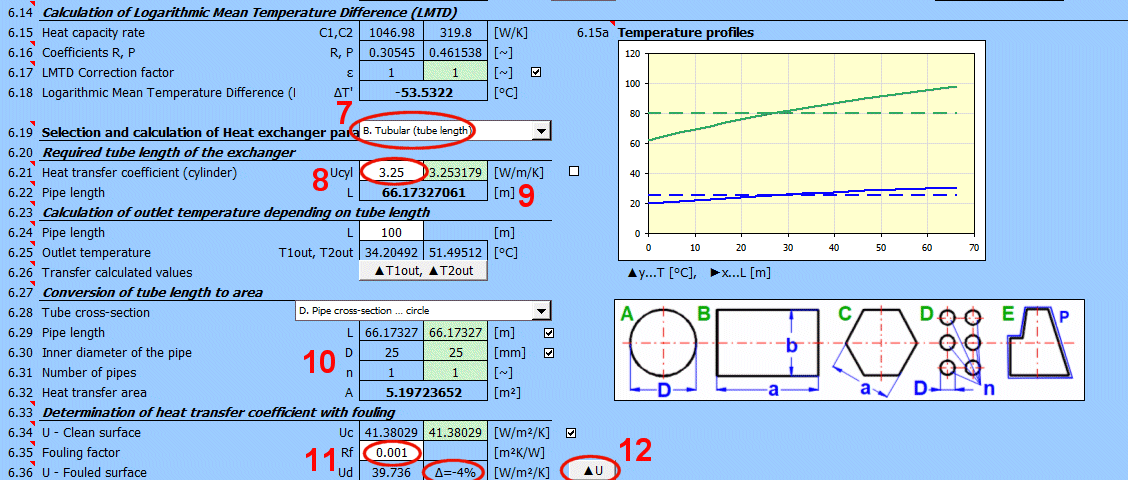
Refroidissement de l'eau dans un radiateur automobile. Le radiateur est
constitué de 40 tubes d'un diamètre intérieur D1=5 mm et d'une longueur L=650
mm, qui traversent des plaques minces étroitement disposées.
L'eau entrant dans l'échangeur de chaleur a une température T1in=90 °C et une
température de sortie T1Out=65 °C. Le débit d'eau est de m1'=0,6 kg/s. L'air
entre dans l'échangeur à T2in=20 °C et a une température de sortie T2Out=40 °C.
Déterminez le débit d'air à travers l'échangeur m2'=??, la puissance Q=?? et le coefficient global de transfert de chaleur U=??, qui doivent être atteints pour satisfaire l'exigence dimensionnelle de 40 tubes d'une longueur de 650 mm.
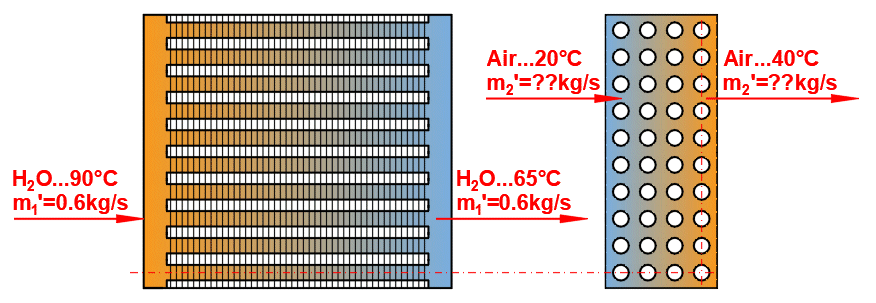

1. Sélectionnez le type d'échangeur de chaleur.
2. Si vous décidez de charger des données à partir de la définition de la paroi
dans la section [4.0], sélectionnez la définition appropriée et chargez avec le
bouton "Load".
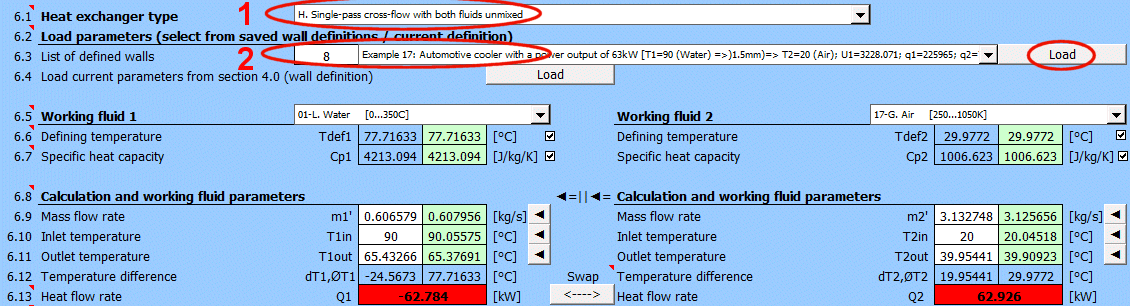
3. Sélectionnez les fluides de travail 1 et 2. Si non dans la liste, entrez
directement la valeur de Cp [6.7].
4. Entrez les paramètres du fluide 1.
5. Entrez les paramètres du fluide 2.
Les valeurs Q1 et Q2 [6.13] seront très probablement différentes et marquées en
rouge. Il est nécessaire de résoudre le bilan énergétique. Dans les champs verts
se trouvent les valeurs calculées qui, lorsqu'elles sont utilisées, garantissent
que Q1=-Q2.
6. Appuyez sur le bouton qui transfère la valeur de conception à m2'. Le débit
d'air de refroidissement m2'=3,14 kg/s.
La puissance de refroidissement du radiateur est de 63 kW.
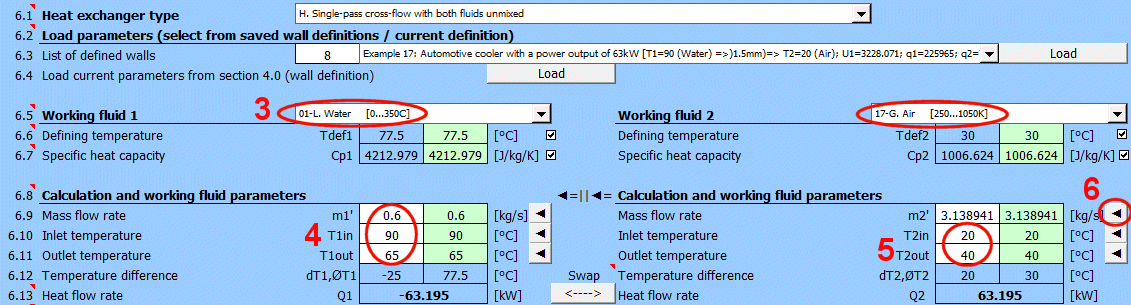
Après avoir résolu le bilan énergétique, il est possible de calculer le
coefficient global de transfert de chaleur requis. Il peut s'agir du Upl
[W/m²/K] rapporté à la surface interne des tubes ou du coefficient Ucyl [W/m/K]
rapporté à la longueur du tube. Dans ce cas, nous choisirons la solution basée
sur la surface (A).
Calcul de la surface. A = D1 * 3,14159 * L * n = 0,005 * 3,14159 * 0,65 * 40 =
0,4084 m^2.
7. Pour les échangeurs de chaleur de type C-H, il est nécessaire d'utiliser un
coefficient de correction ε. Le coefficient est automatiquement suggéré à partir
des températures d'entrée et de sortie.
8. Sélectionnez le type de calcul A. Dans ce cas, il est nécessaire de
déterminer Upl [W/m²/K] pour atteindre la surface définie A.
9. Modifiez progressivement la valeur de Upl jusqu'à ce que la taille de surface
correspondante A = 0,4084 m^2 soit atteinte.
10. Vous pouvez vérifier la taille correcte en convertissant la surface A en
longueur de tube.
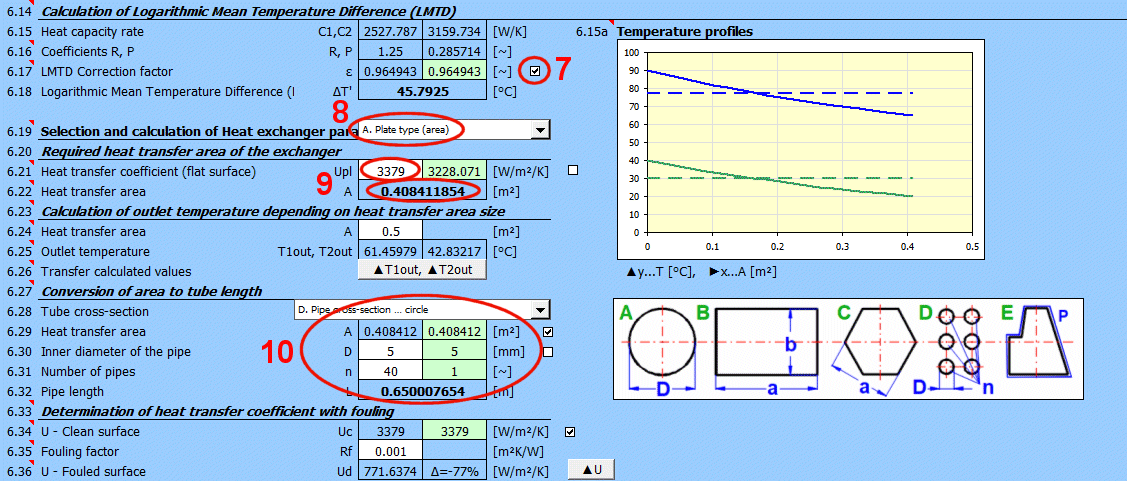
Dans l'exemple 11, nous devons déterminer le flux thermique mutuel entre deux cylindres concentriques entre lesquels il y a un vide. La température de la paroi du cylindre intérieur est T1=99 °C, la température de la paroi du cylindre extérieur est estimée à T2=30 °C.

Déterminez le flux thermique spécifique q21, qui est nécessaire pour résoudre l'exemple 11.
1. Sélectionnez deux surfaces parallèles.
2. Sélectionnez le type de surface, ou entrez directement l'émissivité
ε1=ε2=0,15 à [7.5].
3. Entrez la température T1=99 °C.
4. Entrez la température T2=30 °C (première estimation).
5. Entrez les dimensions des surfaces cylindriques.
6. Le flux thermique spécifique résultant q21=47 [W/m²].
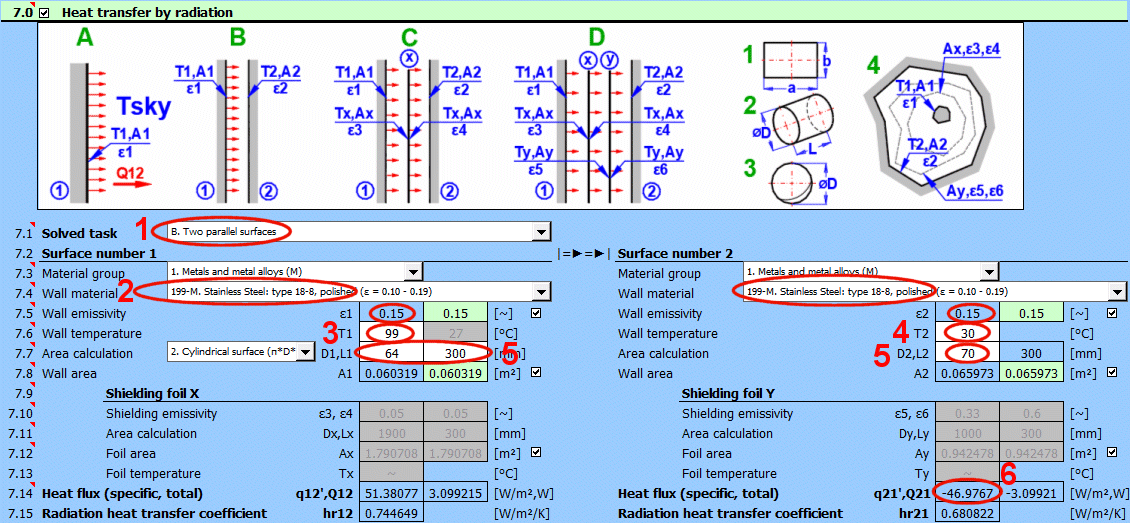
Après avoir substitué la valeur q21=47 [W/m²] dans le calcul du transfert de
chaleur à travers la paroi dans la section [4.0], nous obtenons la température
exacte de la paroi T2=33 °C.
Après avoir réintroduit T2=33 °C dans ce calcul, nous obtenons une valeur plus
précise q21=45 [W/m²].
Un tuyau d'un diamètre D1=200 mm, d'une température de surface T1=200 °C et
d'une émissivité ε1=0,93 est placé concentriquement dans un tunnel circulaire
d'un diamètre D2=2000 mm, d'une température de surface T2=20 °C et d'une
émissivité ε2=0,736. L'écran entre les surfaces est réalisé à l'aide d'une fine
feuille d'aluminium placée concentriquement avec une émissivité ε3=ε4=0,05.
Déterminez le flux thermique entre le tuyau et le tunnel par 1 m de sa longueur.
A) Sans écran.
B) Le film de protection a un diamètre Dx=300 mm.
C) Le film de protection a un diamètre Dx=1900 mm.

1. Sélectionnez le type de problème à résoudre.
2. Entrez l'émissivité des surfaces 1 et 2.
3. Sélectionnez le type de surface à résoudre.
4. Entrez la température et les dimensions de la surface 1 (tuyau). Entrez la
longueur 1 m.
5. Entrez la température et le diamètre du tunnel circulaire (la longueur est la
même).
6. Flux thermique par 1 m de tuyau Q=1370 W.
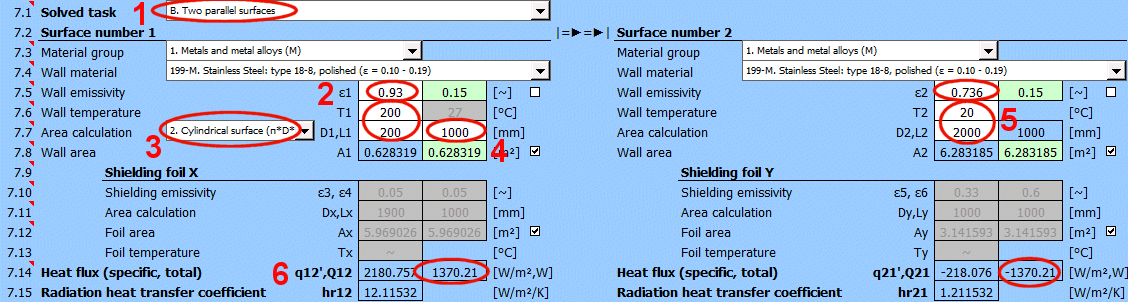
Les valeurs pour les parois 1 et 2 restent les mêmes.
1. Changez le type de problème à résoudre pour C.
2. Entrez l'émissivité du film ε3, ε4.
3. Entrez le diamètre du film de protection Dx=300 mm.
4. Flux thermique par 1 m de tuyau Q=56 W.
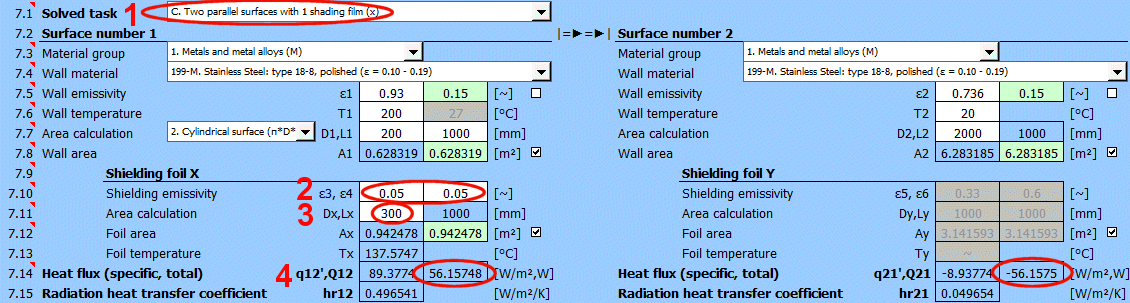
Les valeurs pour les parois 1 et 2 restent les mêmes, seul le diamètre Dx
change.
1. Entrez le diamètre du film de protection Dx=1900 mm.
2. Flux thermique par 1 m de tuyau Q=292 W.

Conclusion : L'utilisation d'un film de protection peut être un moyen efficace de réduire le transfert de chaleur.
Vous concevez une canalisation à travers laquelle un liquide de refroidissement s'écoulera. Votre position est près de Paris dans une zone industrielle. Vous devez déterminer le rayonnement thermique solaire maximal et l'apport énergétique quotidien total.
1. L'intensité maximale du rayonnement solaire est le 21 juin à 12h00.
2. La latitude géographique de Paris est \zeta = 48,9 °.
3. Réglez l'inclinaison de la surface perpendiculairement au soleil \beta=30 °.
4. Réglez l'orientation de la surface au sud \gamma=0 °.
5. L'altitude de Paris est Alt=35 m.
6. Coefficient de pollution de l'air dans la zone industrielle Z=5.
7. Niveau maximal de rayonnement solaire pour un ciel sans nuages dans les
conditions choisies.
8. Apport énergétique quotidien total sur une surface plane définie (aux points
3 et 4). L'apport sur une surface cylindrique sera légèrement plus élevé.
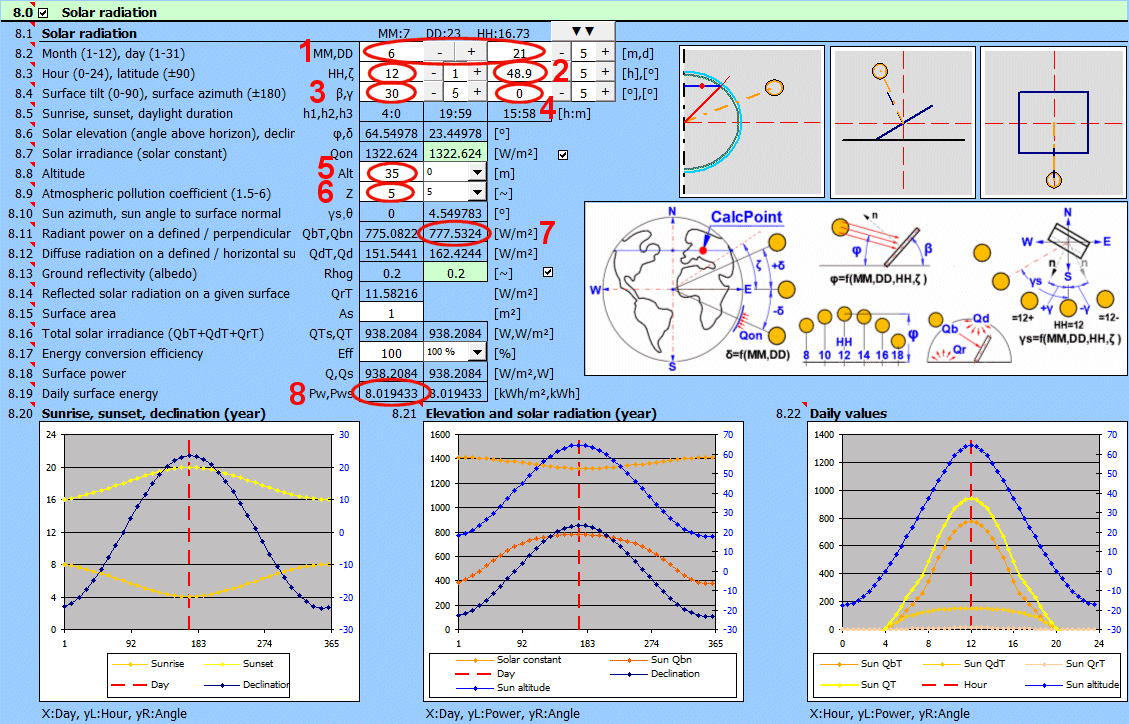
Dans un bâtiment de service avec un toit plat (plan 5 x 14 m).
Surfaces des murs : Définies dans la figure.
Coefficients globaux de transfert de chaleur : Définis dans le tableau.
Conditions extérieures : T4=-10 °C, vent 10 m/s.
Températures et conditions requises : T1=12 °C, T2=22 °C, T3=15 °C.
Conditions d'entrée : sources de chaleur QH1=1000 W, QH2=2000 W, QH3=1500 W.
Les deux problèmes peuvent être résolus avec le même modèle mathématique.
Dans la section [4.0], les coefficients globaux de transfert de chaleur U pour
les murs individuels sont calculés et enregistrés dans la liste des murs
résolus.
1. Définissez quelles valeurs des murs résolus seront transférées dans le
tableau.
2. Chargez successivement les informations des murs pour chaque pièce.
Bien sûr, il est possible d'entrer les valeurs U directement, par exemple à
partir du catalogue du fournisseur.
3. Définissez la surface réelle de chaque mur selon la figure (A1=26,6,
A2=6,4,.....).
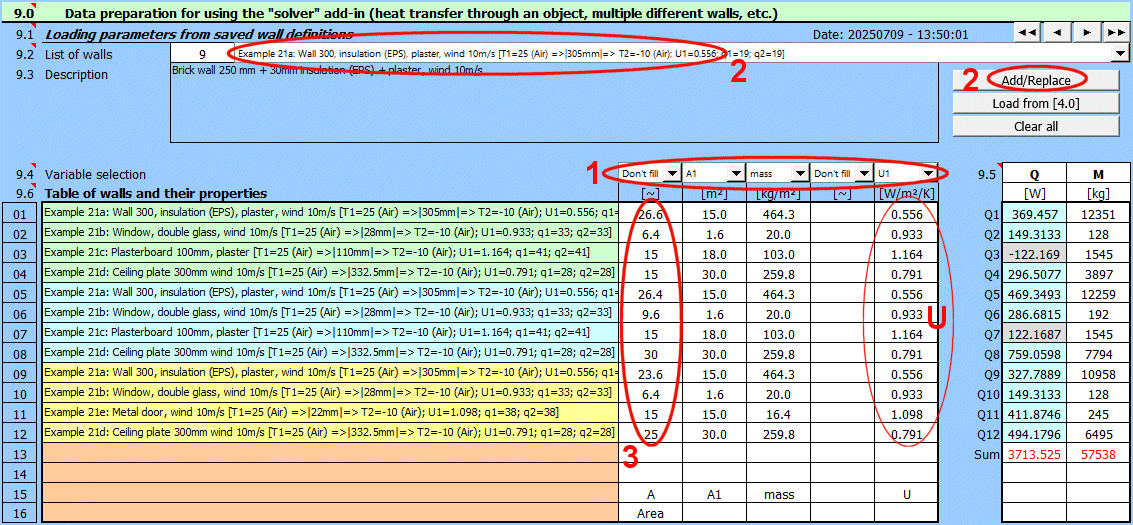
4. Définissez dans la colonne Q le flux thermique pour chaque paroi selon la
formule Q = \Delta T * A * U (\Delta T ... différence de température, A ...
surface de la paroi, U ... coefficient global de transfert de chaleur).
Q1 = (T1 - T4) * A1 * U1
Q2 = (T1 - T4) * A2 * U2
Q3 = (T1 - T2) * A3 * U3
Q4 = (T1 - T4) * A4 * U4
............
5. Définissez les conditions qui stipulent que le flux thermique de chaque pièce
doit être égal à la puissance de la source de chaleur.
Q1+Q2+Q3+Q4-QH1=0
Q5+Q6+Q7+Q8-Q3-QH2=0
Q9+Q10+Q11+Q12-Q7-QH3=0
6. Définissez des valeurs initiales appropriées pour les sources de chaleur (par exemple, QH1=500, QH2=1500, QH3=1500).
7. Définissez les températures requises selon l'énoncé.
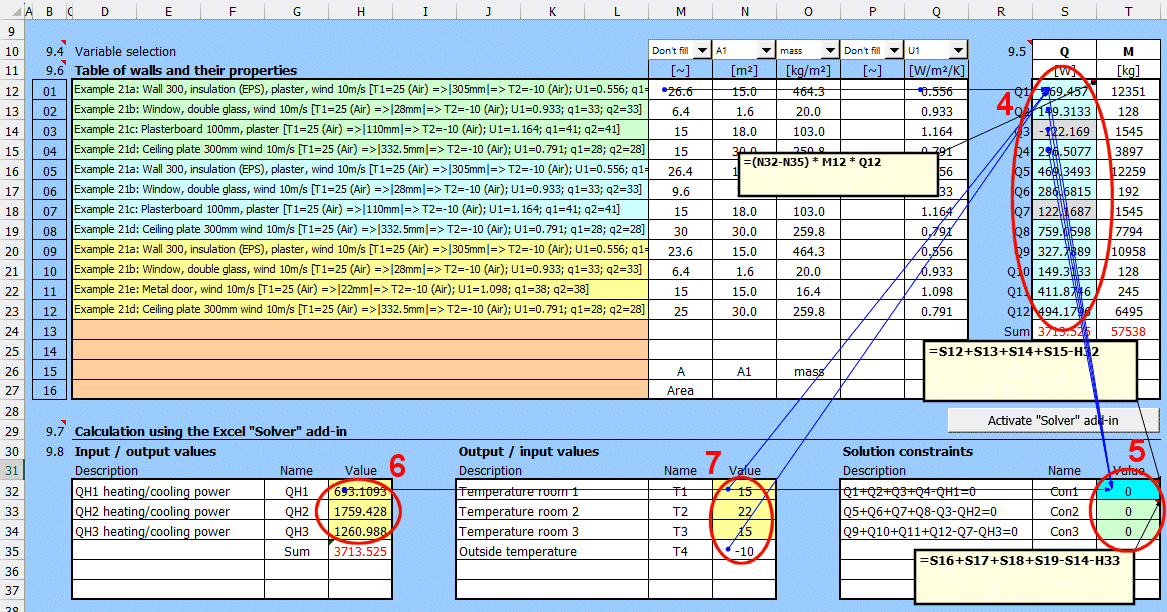
1. Lancez le complément "Solveur" (Menu Excel "Données").
2. Entrez la cellule et la valeur à atteindre : "Définir l'objectif :".
3. Entrez les cellules à modifier : "En modifiant les cellules variables :".
4. Ajoutez d'autres conditions à respecter : "Sous contrainte :".
5. Lancez la résolution du problème : "Résoudre".
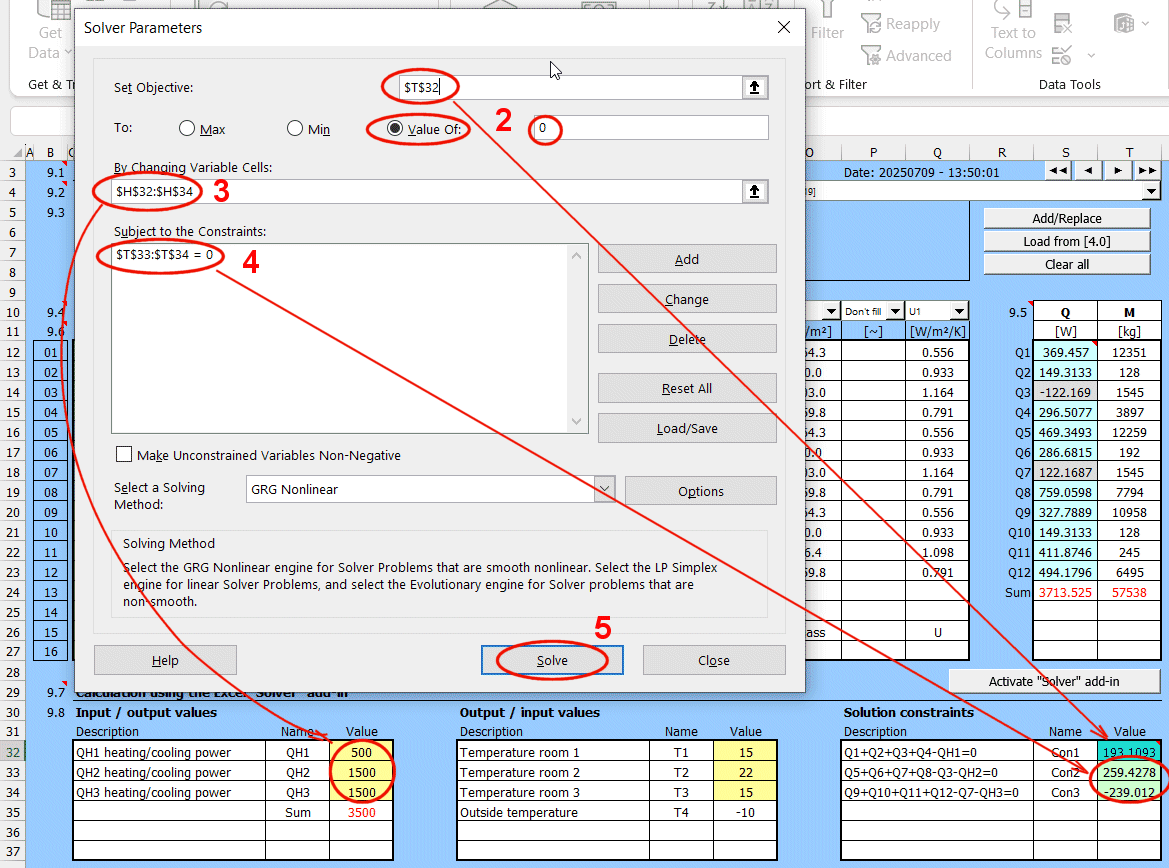
À la fin de la résolution, les valeurs requises (3) et (4) devraient changer, et
une boîte de dialogue apparaîtra.
1. Choisissez de conserver la solution.
2. Confirmez : "OK".
3,4. Résultats de la solution.
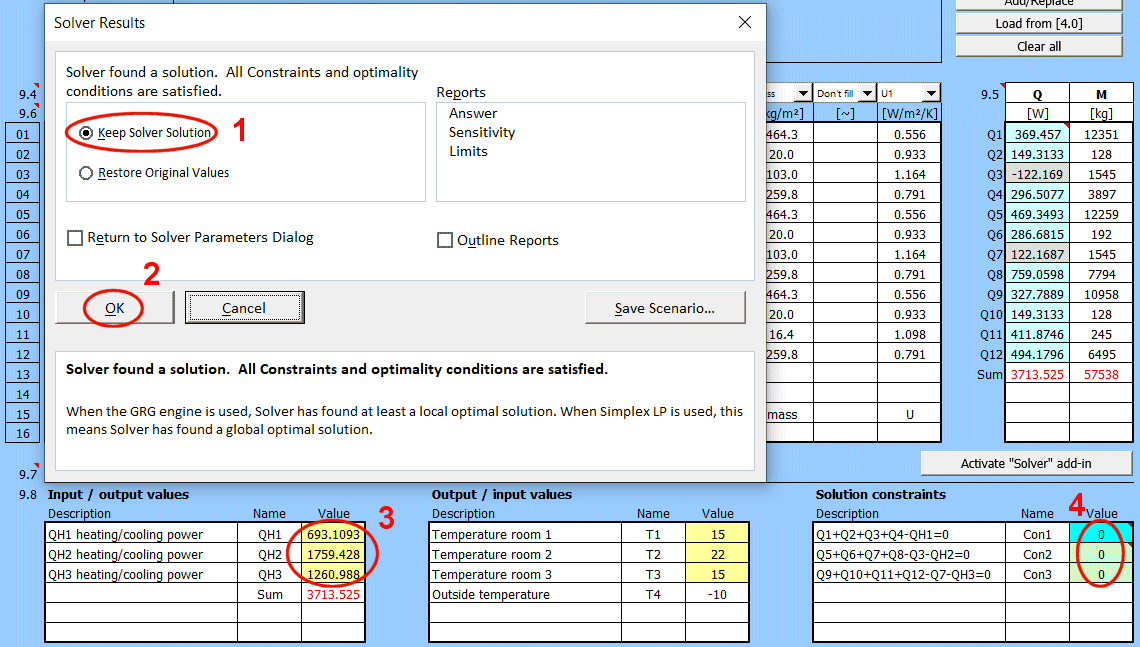
La tâche B est résolue de la même manière, où pour les puissances de chauffage données (3), les températures des pièces T1, T2, T3 sont modifiées.
L'information sur le réglage des paramètres de calcul et le choix de la langue peut être trouvée dans le document "Réglage des calculs, changement de langue".
Les informations générales sur la façon dont vous pouvez modifier et prolonger les cahiers de travail du calcul sont mentionnées dans le document "Modifications du cahier de travail (calcul)".
Littérature:
EN
[01] YUNUS A. ÇENGEL, AFSHIN J. GHAJAR: Heat and Mass Transfer: Fundamentals
& Applications, 5th Edition, McGraw-Hill Education.
[02] YUNUS A. ÇENGEL: Heat Transfer a Practical Approach, Second Edition.
[03] MORAN, M.J., SHAPIO, H.N.: Fundamentals of engineering thermodynamics. 8th
Edition New York: John Wiley a sons, 1990.
[04] DEWITT, BERGMAN, LAVINE: Fundamentals of Heat and Mass Transfer 6th Edition
[05] WARREN M.ROHSENOW, JAMES R.HARTNETT, YOUNG I.CHO: Handbook of Heat
Transfer, 3th Edition, McGraw-Hill
[06] SCHLUNDER, BELL, HEWITT, SPALDING: Heat Exchanger
Design Handbook, VDI-Verlag GmbH, 1983.
[07] LOIS THEODORE: Heat Transfer Applications for the
Practicing Engineer, John Wiley & Sons, Inc., 2011.
[08] MYER KUTZ: Heat-Transfer Calculations, McGraw-Hill
[09] HOLMAN, J.P.: Heat Transfer, 10th. Edition, New
York: McGraw-Hill
[10] HOLMAN, J.P. Thermodynamics. 4th. New York:
McGraw-Hill Book Company, 1988. 780 s. ISBN 0-07-029633-2.
[11] MOHAMED M. EL-AWAD: Optimisation Analyses of
Fluid- Thermal Systems Using Excel,
[12] FRANK KREITH, RAJ MANGLIK, MARK BOHN: Principles
of Heat Transfer, Cengage Learning, Inc., 2011
CZ
[13] HORÁK VLADIMÍR, STŘEDA IVO: Mechanika tekutin
- Termomechanika, Strojírenská příručka, Scientia sro.
[14] RANEVI,K. Termodynamické tabulky. 1.vyd.
Bratislava: ALFA 1984. 313s. [L5] HAEK, P. Tabulky pro tepelnou techniku. 1 .vyd.
VB Ostrava, 1980, 247 s.
[15] SAZIMA,M., KMON1OEK,V., SCHNELER,J. Teplo. 1.vyd.
Praha: SNTL, 1989. 588 s. Technický průvodce. ISBN 80-03-00043-2.
[16] M.A.MICHEJEV: Základy sdílení tepla, Průmyslové
vydavatelství, 1952
[17] PETRAK,J., DVOAK, Z., KLAZAR, L., SYNEK, V.
Chiadivo R134a, (1.vyd.) VUT, 1993. 72s.
[18] MIROSLAV JÍLEK, ZDENĚK RANDA: Termomechanika -
sbírka příkladů, ČVUT, 2004
Normes:
ASTM C1340-2015 ... Estimation of Heat Gain or Loss Through Ceilings Under
Attics Containing Radiant Barriers...
ISO 12241:2022
Tepelněizolační výrobky pro zařízení budov a průmyslové instalace - Pravidla
výpočtu
Thermal insulation for building equipment and industrial installations —
Calculation rules
Isolation thermique des équipements de bátiments et desinstallations
industrielles — Méthodes de calcul
Wärmedammung an haus- und betriebstechnischen Anlagen — Berechnungsregeln
^